Penjumlahan matriks
Misalkan terdapat dua buah matriks, yaitu matriks A dan matriks B. Jika matriks C adalah matriks penjumlahan dari A dengan B, maka matriks C dapat diperoleh dengan menjumlahkan setiap elemen pada matriks A yang seletak dengan setiap elemen pada matriks B. Oleh karena itu, syarat agar dua atau lebih matriks dapat dijumlahkan adalah harus memiliki ordo yang sama.
Contoh:
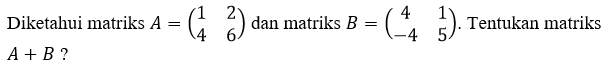
Hasil dari A + B dapat diperoleh dengan menjumlahkan setiap elemen matriks A yang seposisi dengan setiap elemen matriks B.
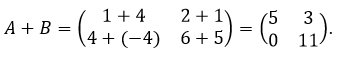
A = [aij], lawan matriks A ditulis -A = [-aij]
Pengurangan matriks
Misalkan terdapat dua buah matriks, yaitu matriks A dan matriks B. Jika matriks C adalah matriks pengurangan dari A dengan B, maka matriks C dapat diperoleh dengan mengurangkan setiap elemen pada matriks A yang seletak dengan setiap elemen pada matriks B.
Pada dasarnya, pengurangan sama halnya dengan penjumlahan terhadap lawan bilangan penambah, sehingga pengurangan matriks A dengan matriks B dapat diartikan sebagai penjumlahan matriks A dengan lawan matriks B.
A – B = A + (-B)
Sama halnya dengan syarat penjumlahan matriks, dua atau lebih matriks hanya dapat dikurangkan apabila memiliki ordo yang sama, teman-teman. Nah, supaya kamu nggak bingung, kita coba kerjakan contoh soal di bawah ini, yuk. Gaasss~
Contoh:
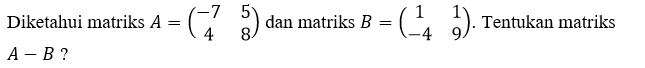
Hasil dari A – B dapat diperoleh dengan mengurangkan setiap elemen matriks A yang seposisi dengan setiap elemen matriks B.
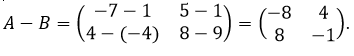
Perkalian matriks dengan bilangan real (skalar)
Misalkan terdapat matriks A berordo m × n dan suatu bilangan real (skalar), yaitu k. Perkalian antara matriks A dengan skalar k dapat ditulis dengan kA yang diperoleh dengan mengalikan setiap elemen matriks A dengan skalar k.
Perkalian suatu matriks dengan skalar dapat dilakukan tanpa syarat tertentu. Artinya, semua matriks dengan ordo sembarang dapat dikalikan dengan bilangan real (skalar).
Perkalian matriks dengan matriks
Misalkan terdapat dua buah matriks, yaitu matriks A dengan ordo m × p dan matriks B dengan ordo p × n. Perkalian matriks A dengan matriks B dapat ditulis dengan A × B yang diperoleh dari penjumlahan hasil kali elemen-elemen yang bersesuaian pada baris ke-i matriks A dengan kolom ke-j matriks B, dengan i = 1, 2, 3, …, m dan j = 1, 2, 3, …, n.
Syarat agar dua buah matriks dapat dikalikan adalah matriks pertama harus memiliki jumlah kolom yang sama dengan jumlah baris pada matriks kedua. Ordo matriks hasil perkalian dua buah matriks adalah jumlah baris pertama dikali jumlah kolom ke dua.
Contoh:
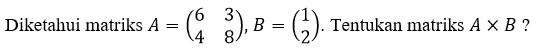
Jumlah kolom matriks A adalah 2 dan jumlah baris matriks B adalah 2. Matriks A memiliki jumlah kolom yang sama dengan jumlah baris matriks B, sehingga syarat perkalian antarmatriks sudah terpenuhi.






Post a Comment