Ukuran pemusatan data merupakan salah satu pengukuran data dalam statistika. Statistika adalah pengetahuan yang berhubungan dengan cara mpenyusunan data, penyajian data, dan penarikan kesimpulan mengenai suatu keseluruhan berdasarkan data yang ada pada bagian dari keseluruhan tadi. Yang termasuk dalam ukuran pemusatan data adalah rataan (Mean), Median, Modus . Untuk memudahkan anda dalam memahami materi ini, dibawah ini akan kita uraikan penjelasan dibawah ini.
Ukuran Pemusatan Data
Rataan (Mean)
Mean atau rata-rata hitung adalah nilai yang diperoleh dari jumlah sekelompok data dibagi dengan banyaknya data. Rata-rata disimbolkan dengan x.
- Rata-Rata untuk Data Tunggal
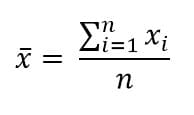
Keterangan:
ẋ = mean
n = banyaknya data
xi= nilai data ke-i
Nilai ulangan matematika 15 siswa kelas XIIPAadalah 7,8,6,4,10, 5,9,7, 3,8, 6, 5, 8, 9, dan 7. Tentukan nilai rata-ratanya.
Jawab:
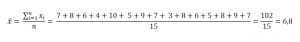
Jadi, nilai rata-ratanya adlah 6,8
- Rata-Rata untuk Data Bergolong (Berkelompok)
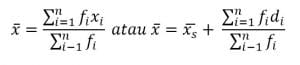
Keterangan:
xi = nilai tengah data ke-i
fi = frekuesni data ke -i
xs = rataan sementara (dipilih pada interval dengan frekuensi terbesar)
di = simpangan ke-i (selisih nilai xi dengan nilai xs)
Tentukan rata-rata dari data berikut.
[table id=1 /]
Jawab:
Cara I:
[table id=2 /]
Penyelesaian:
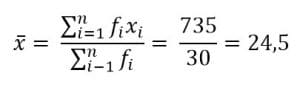
Cara II:
[table id=3 /]
Penyelesaian:
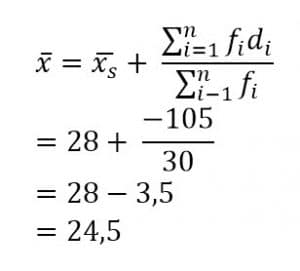
Median
Median adalah nilai data yang terletak di tengah setelah data diurutkan. Dengan demikian, median membagi data menjadi dua bagian yang sama besar. Median (nilai tengah) disimbolkan dengan Me.
- Median untuk Data Tunggal
1. Jika banyaknya data n ganjil maka median
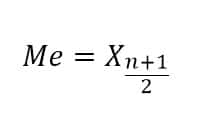
2. Jika banyaknya n genap maka
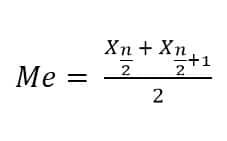
Tentukan median dari data berikut.
- 8,6,4,3,7,5,8,10,8,9,8,5
| Nilai | 3,4,5,6,7,8,9 |
| Frekuensi | 2,5,7,8,10,5,4 |
Jawab:
- Data diurutkan : 3 4 5 5 6 7 8 8 8 8 9 10
N= 12 (genap)
Jadi, mediannya adlah 7,5
- n = 41 (ganjil)
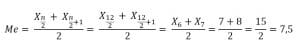
- Median untuk data bergolong
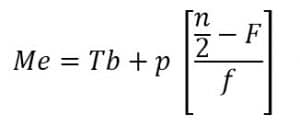
Keterangan:
Me = median
Tb = tepi bawah kelas median
p = panjang kelas
n = banyak data
F = frekuensi kumulatif sebelum kelas median
f = frekuensi kelas median
Tentukan median dari data berikut.
[table id=4 /]
Jawab:
Karena banyaknya data adlah 36 maka median terletak diantara data ke-18 dan data ke-19 sehingga diperoleh kelas yang mengandung median adalah 4-40. Dengan demikian , Tb = 41-0,5 = 40,5; p=10 (11-20); f =7; F= 16.
[table id=5 /]
Penyelesaian:
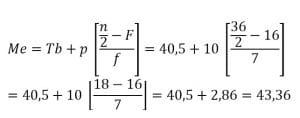
Jadi, mediannya adlah 43,36
Modus
Modus adalah data yang paling sering muncul atau memiliki frekuensi tertinggi. Modus dilambnagnkan dengan Mo.
- Modus untuk data tunggal
Modus dari data tunggal adalah data yang paling sering muncul.
Tentukan modus dari data : 7,6,5,8,3,7,9,4,6,4,8,4,10,7,5,7,dan 8.
Jawab:
Data diurutkan: 3,4,4,4,5,5,6,6,7,7,7,7,8,8,8,9,10.
Nilai 7 muncul paling banyak, yaitu 4 kali.
Jadi, modusnya adalah 7.
- Modus untuk data bergolong
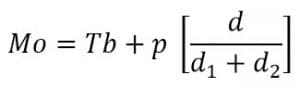
Keterangan :
Mo : modus
Tb : tepi bawah kelas modus
p : panjang kelas
d1 : selisih frekuensi kelas modus dengan kelas sebelumnya
d2 : selisih frekuensi kelas modus dengan kelas sesudahnya
Tentukan modus dari data berikut
[table id=6 /]
Jawab:
Karena kelas dengan frekuensi terbanyak 9 maka modus terletak diantara kelas 51-60; tb=51-0,5=50,5; p=10(11-20); di=9-4=5; F=16.
Penyelesaian:
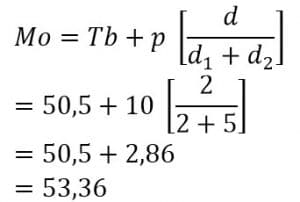
Jadi, modusnya adalah 53,36


Post a Comment