Ukuran penyebaran data
Dalam pengukuran statistika terdpat pula Ukuran Penyebaran data. Ukuran penyebaran data merupakan ukuran yang menunjukkan seberapa jauh data menyebar dari rata-rata. Terdapat ukuran penyebaran data yang akan kita pelajari pada artikel ini, yaitu Jangkauan (range), Simpangan rata-rata, Ragam (variasi), dan Simpangan Baku. namun, sebelum anda mempelajari postingan ini, sebaiknya anda baca dulu materi sebelumnya tentang pengertian Statistika, Ukuran Pemusatan data Dan Ukuran Letak Data.
Penjelasan dan uraian lengkapnya akan dijelaskan pada penjelasan di bawah ini.
Jangkauan (Range)
Jangkauan merupakan selisih data terbesar dan data terkecil. Jangkauan sering dilambangkan dengan R.
1. Jangkauan Data
R = xmaks – xmin
Keterangan:
R = jangkauan
Xmaks = data terbesar
Xmin = data terkecil
Tentukan jangkauan dari data : 3,6,10,5,8,9,6,4,7,5,6,9,5,2,4,7,8.
Jawab :
R = xmaks – xmin
= 10-2 = 8
Jadi, jangkaun data tersebut adalah 8.
2. Jangkauan interkuartil
Jangkauan interkuartil adalah selisih antara kuartil ketiga dan kuartil pertama.
H = Q3 – Q1
Keterangan :
H = jangkauan interkuartil
Q3 = kuartil ketiga
Q1 = kuartil pertama
3. Simpangan kuartil ( jangkauan semi interkuartil)
Singan kuartil adalah setengah dari selisih kuartil ketiga dan kuartil pertama.
Sk = ½ Q3 – Q1
Keterangan :
Sk = simpangan kuartil
Q3 = kuartil ketiga
Q1 = kuartil pertama
Simpangan Rata- Rata
Simpangan rata-rata merupakan nilai rata-rata dari selisih setiap data dengan nilai mean atau rataan hitungnya. Simpangan rata-rata sering dilambangkan dengan SR.
1. Data Tunggal
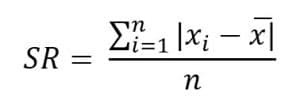
Keterangan :
SR = simpangan rata-rata
Xi = data ke-i
X = rataan hitung
n = banyak data
Tentukan simpangan rata-rata dari data 4,6,8,5,4,9,5,7.
Jawab :
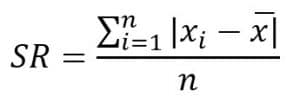
![]()
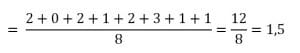
Jadi, simpangan rata-ratanya adalah 1,5
2. Data Bergolong (Berkelompok)
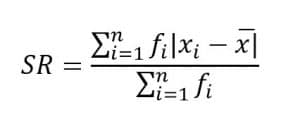
Keterangan :
SR = simpangan rata-rata
Xi = data ke-i
X = rataan hitung
fi = frekuensi data ke-i
Tentukan simpangan rata-rata dari data berikut:
| Data | f |
| 41-45 | 6 |
| 46-50 | 3 |
| 51-55 | 5 |
| 56-60 | 8 |
| 61-65 | 8 |
Jawab:
| Data | f | xi | fixi | |xi-x| | Fi|xi-x| |
| 41-45 | 6 | 43 | 258 | 11,5 | 69 |
| 46-50 | 3 | 48 | 114 | 6,5 | 19,5 |
| 51-55 | 5 | 53 | 265 | 1,5 | 7,5 |
| 56-60 | 8 | 58 | 464 | 3,5 | 28 |
| 61-65 | 8 | 63 | 504 | 8,5 | 68 |
| Jumlah | 30 | 1.635 | 165 |
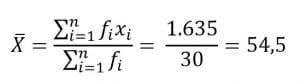
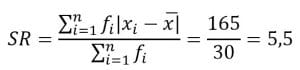
Jadi, simpangan rata-ratanya adalah 5,5.
Ragam
Ragam atau variasi adlah nilai yang menunjukkan besarnya penyebaran data pada kelompok data. Ragam atau variasi dilambangkan dengan s2.
1. Variasi untuk data tunggal
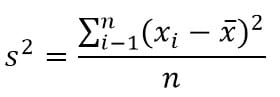
Keterangan :
s2= variasi
xi = data ke –i
x = rataan hitung
n = banyak data
2. Variasi untuk data bergolong (berkelompok)
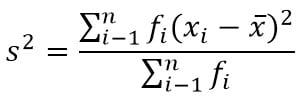
Keterangan :
s2= variasi
xi = data ke –i
x = rataan hitung
fi = frekuensi data ke-i
Simpangan baku
Simpangan baku atau disebut juga deviasi standar merupakan akar dari jumlah kuadrat diviasi dibagi banyaknya data. Simpangan baku sering dilambangkan dengan s.
1. Simpangan baku untuk data tunggal
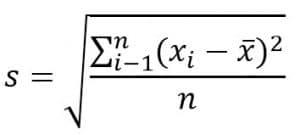
Keterangan :
S = simpangan baku
xi = data ke –i
x = rataan hitung
n = banyak data
2. Simpangan baku untuk data bergolong (berkelompok)
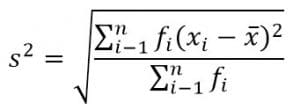
Keterangan :
s = simpangan baku
xi = data ke –i
x = rataan hitung
fi = frekuensi data ke-i
Tentukan variari dan simpangan baku dari data : 4,6,8,7,9,8.
| Data | f |
| 41-45 | 6 |
| 46-50 | 3 |
| 51-50 | 5 |
| 56-60 | 8 |
| 61-65 | 8 |
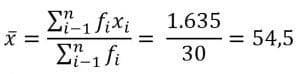
Jawab :
| Data | f | xi | fixi | (xi-x)2 | fi(xi-x)2 |
| 41-45 | 6 | 43 | 258 | 132.25 | 93.5 |
| 46-50 | 3 | 48 | 144 | 42.25 | 126.75 |
| 51-50 | 5 | 53 | 265 | 2.25 | 11.25 |
| 56-60 | 8 | 58 | 464 | 12.25 | 98 |
| 61-65 | 8 | 63 | 504 | 72.25 | 578 |
| Jumlah | 30 | 1.635 | 676 |
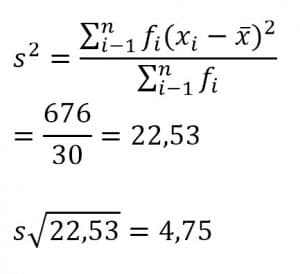
Jadi, variasinya = 22,53 dan simpangan bakunya = 4,75.


Post a Comment