Materi Persiapan Ujian Akhir Sekolah

Table of Contents

 

1. Perpangkatan dan Akar 

Bilangan berpangkat adalah suatu bilangan yang digunakan sebagai bentuk penyederhanaan dari sebuah bilangan yang mana bilangan tersebut mempunyai faktor-faktor perkalian yang sama.

Bentuk akar adalah bilangan yang jika dimasukkan dalam operasi bentuk akar menghasilkan bilangan irasional. Bentuk akar termasuk ke dalam bilangan irasional dimana bilangan irasional tidak bisa disebutkan dengan menggunakan bilangan pecahan a/b, a serta b bilangan bulat a dan b tidak sama dengan 0

 2. Barisan dan Deret

Barisan aritmetika adalah barisan bilangan yang memiliki selisih yang sama di antara suku-sukunya yang saling berdekatan. Selisih ini bisa kita sebut dengan beda, simbolnya b, ya. Kalau deret aritmetika adalah jumlah suku ke-n pertama pada barisan aritmatika.

 3. Matriks

Matriks adalah sekumpulan bilangan yang disusun berdasarkan baris dan kolom, serta ditempatkan di dalam tanda kurung. Nah, tanda kurungnya ini bisa berupa kurung biasa “( )” atau kurung siku “[ ]”, ya. Suatu matriks diberi nama dengan huruf kapital, seperti A, B, C, dan seterusnya.

4. Fungsi Kuadrat 

Fungsi kuadrat adalah sebuah fungsi polinom yang memiliki peubah/variabel dengan pangkat tertingginya adalah 2 (dua). Secara umum fungsi kuadrat memiliki bentuk umum seperti berikut ini:  f(x) = ax2 + bx + c, a ≠ 0 dengan f(x) = y yang merupakan variabel terikat, x adalah variabel bebas, sedangkan a, dan b merupakan koefisien dan c adalah suatu konstanta.

5. Peluang

Peluang suatu kejadian itu adalah kemungkinan dari suatu kejadian. Selain peluang lolos di kampus impian, banyak contoh lain tentang peluang, ya. Bisa peluang mendapatkan bola berwarna merah, peluang menang lomba, peluang turun hujan, dan masih banyak lagi.

Materi Selengkapnya berikut ini 

6. Kalkulus

Kalkulus adalah cabang ilmu matematik yang merangkumi had, terbitan, kamiran, dan deret tak terhingga. Kalkulus adalah ilmu mengenai perubahan, sebagaimana geometri adalah ilmu mengenai bentuk dan algebra adalah ilmu mengenai pengerjaan untuk memecahkan persamaan serta aplikasinya. Kalkulus mempunyai aplikasi yang luas dalam bidang-bidang sains, ekonomi, dan teknikal; serta dapat menyelesaikan pelbagai masalah yang tidak dapat diselesaikan dengan algebra asas. Kalkulus mempunyai dua cabang utama, iaitu kalkulus pembezaan dan kalkulus kamiran yang saling berhubungan melalui teorem asas kalkulus. Pelajaran kalkulus adalah pintu gerbang menuju pelajaran matematik lain yang lebih tinggi, yang khusus mempelajari fungsi dan limit, yang secara umum dinamakan analisis matematik.

Pengertian Kalkulus

Kalkulus merupakan salah satu topik bahasan dalam matematika. Topik pembahasan kalkulus meliputi konsep limit, diferensial atau turunan, serta integral atau anti-turunan.

Pembahasan mengenai konsep-konsep materi dalam kalkulus akan dijelaskan pada bagian yang lain.

Berikutnya akan disebutkan beberapa contoh penerapan kalkulus dalam kehidupan sehari-hari.

Kalkulus dalam Kehidupan Sehari-hari

Kalkulus memiliki beragam penerapan dalam kehidupan sehari-hari. Matematika sebagai salah satu induk ilmu pengetahuan sangat dibutuhkan dalam bidang lain.

Beberapa penerapan kalkulus dalam bidang lain antara lain:

• Pada bidang fisika, khusunya terkait mekanika, kalkulus sangat diperlukan untuk menyelesaikan perhitungan-perhitungan dengan menerapkan konsep kalkulus.
• Dalam bidang statistika dan teori peluang juga terdapat perhitungan dengan menerapkan konsep kalkulus (integral).
• Dalam bidang ekonomi, kalkulus dapat digunakan untuk menentukan biaya marginal (kalkulus diferensial).

Dan masih banyak lagi bidang-bidang yang menerapkan konsep kalkulus.

Selanjutnya akan dijelaskan mengenai kalkulus dasar.

Kalkulus Dasar

Penjelasan mengenai kalkulus dasar pada bagian ini yaitu konsep mengenai limit, turunan (diferensial), dan anti-turunan (integral).

Limit

Misalkan terdapat suatu fungsi f(x). Limit dapat didefinisikan sebagai suatu nilai fungsi untuk nilai x mendekati suatu bilangan tertentu. Limit dapat dirumuskan sebagai berikut.

Rumus Limit

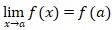
Keterangan:

• x : variabel
• a : suatu bilangan
• f(x) : fungsi dengan variabel x
• f(a) : nilai limit fungsi x mendekati a.

Turunan (Diferensial)

Turunan merupakan lanjutan dari konsep limit. Misalkan terdapat suatu fungsi f(x).

Turunan dapat didefinisikan sebagai suatu perhitungan terhadap perubahan nilai f(x) seiring dengan perubahan dari nilai x.

Turunan dari suatu fungsi f(x) disimbolkan dengan f’(x). Misalkan terdapat f(x) = axn, maka turunan dari fungsi tersebut adalah

Rumus Turunan

f’(x) = anxn-1

Keterangan:

• f(x)  : fungsi dengan variable x
• f’(x) : turunan fungsi f(x)

Anti-turunan (Integral)

Pernahkah kalian mendengar mengenai integral? Integral merupakan kebalikan dari turunan.

Misalkan terdapat suatu fungsi f(x). Integral dari fungsi f(x), disimbolkan dengan F(x) yaitu sebagai berikut.

Rumus Integral

F(x) = ∫ f(x)

Keterangan:

• F(x) : integral dari f(x)
• f(x)  : fungsi dengan variable x.

Misalkan terdapat fungsi f(x) = axn. Integral dari fungsi tersebut adalah

F(x) = ∫ axn = a/(n + 1) xn+1 + C

Keterangan:

• F(x) : integral dari suatu fungsi
• axn : fungsi dengan koefisien a, variabel x, dan pangkat n.
• C : konstanta

Materi Selengkapanya