Pengertian Peluang Suatu Kejadian
Peluang suatu kejadian itu adalah kemungkinan dari suatu kejadian. Selain peluang lolos di kampus impian, banyak contoh lain tentang peluang, ya. Bisa peluang mendapatkan bola berwarna merah, peluang menang lomba, peluang turun hujan, dan masih banyak lagi.
Tapi sebelum kita lanjut, ada beberapa hal atau istilah-istilah dasar yang ada di peluang kejadian ini. Jadi, kamu wajib paham karena istilah-istilah ini akan selalu ada di materi peluang. Beberapa hal atau istilah-istilah dasar yang ada di peluang kejadian ini.
Rumus Peluang Suatu Kejadian
Peluang atau kemungkinan, secara teoritis artinya perbandingan antara banyaknya suatu kejadian dengan banyaknya seluruh kemungkinan yang terjadi. Jadi, kita bisa tuliskan rumus peluang kejadian, Sebagai berikut :
Sifat-sifat Peluang Suatu Kejadian
Contoh
1. Empat bola diambil secara acak dari sebuah box yang berisi 15 buah bola. Karena salah penempatan, 3 bola kempis dan tidak bisa digunakan. Peluang terambilnya empat bola yang tidak kempis adalah….
- 0
- 0,23
- 0,36
- 0,42
- 0,46
Pembahasan:
Dari soal diketahui ada 15 bola dan 3 diantaranya kempis. Jadi, sisa 12 bola yang bisa digunakan.
Nah, karena dari soal tidak ada aturan urutan dalam pengambilan bola, jadi rumus yang kita pakai adalah rumus kombinasi.
Cari n(S) terlebih dahulu:
Banyak cara mengambil 4 bola dari 15 bola adalah
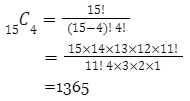
Next, kita cari n(A):
Banyak cara mengambil 4 bola dari 12 bola adalah
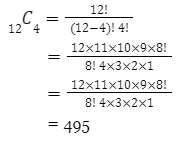
Jadi, peluang 4 bola yang terambil tidak pecah adalah
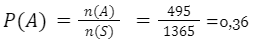
2. Terdapat sebuah kotak yang berisikan 10 buah balon, yang terdiri dari 3 balon merah dan 7 balon kuning. Hitunglah peluang terambil 3 balon kuning sekaligus!
Pembahasan:
Untuk menghitung banyaknya cara pengambilan 3 balon kuning sekaligus dari 7 balon kuning, dapat digunakan rumus kombinasi:
n(A) = 7C3
7C3 = 7! / (7-3)! × 3!
= 7 × 6 × 5 × 4! / 4! × 3 × 2 × 1
= 7 × 6 × 5 × 4! / 4! × 3 × 2 × 1
= 7 × 5 / 1
= 35
Untuk banyaknya cara pengambilan 3 balon dari 10 balon adalah:
n(S) = 10C3
10C3 = 10! / (10-3)! × 3!
= 10 × 9 × 8 × 7! / 7! × 3 × 2 × 1
= 10 × 9 × 8 × 7! / 7! × 3 × 2 × 1
= 720/6
= 120
Lalu, kita hitung peluang terambil 3 balon kuning sekaligus:
P(A) = n(A) / n(S) = 35/120 = 7/24 = 0,29
Jadi, jawaban yang tepat untuk contoh soal peluang acak di atas adalah 0,29.
Pengertian Peluang Komplemen
Di materi peluang kejadian ini, juga ada yang namanya peluang komplemen, simbolnya kayak gini nih Ac. Peluang komplemen sering juga tuh keluar di soal-soal ujian teori peluang. Kalau begitu, apa sih yang dimaksud peluang komplemen? Jadi, peluang komplemen (Ac) adalah peluang semua kejadian yang bukan A.
Rumus Peluang Komplemen
Peluang kejadian punya hubungan dengan peluang komplemen. Dari hubungan itu lah, kita bisa mendapatkan rumus peluang komplemen. Hubungan antara peluang kejadian A dengan komplemennya (Ac), antara lain:
Contoh
1. Diketahui suatu kantong berisi 8 bola merah, 4 bola putih, dan 2 bola hijau. Peluang terambilnya bola bukan merah adalah ….
Pembahasan:
Misal: P(A)= peluang terambilnya bola merah
Maka, untuk mencari peluang terambilnya bola merah atau 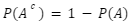
Yuk kita cari terlebih dahulu P(A) dengan rumus:
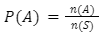
n(A) adalah banyaknya bola merah dalam kantong, berarti n(A)= 8
Sedangkan n(S) banyaknya sampel yaitu jumlah semua bola yang ada di kantong,
n(S) = 8 + 4+ 2 = 14.
langsung aja kita substitusi ke rumus: 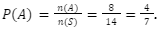
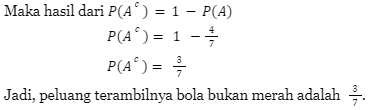
2. Tiga uang koin dilempar secara bersamaan. Peluang tidak muncul gambar satu pun adalah…
Pembahasan:
Misal: P(A) = peluang munculnya gambar
Maka, untuk mencari peluang tidak muncul gambar adalah P(Ac) = 1 – P(A)
Cari terlebih dahulu P(A) dengan rumus:
P(A) = n(A) / n(S)
n(A) adalah banyaknya gambar yang ada pada ruang sampel, berarti n(A) = 7
Sedangkan n(S) adalah banyaknya sampel, berarti n(S) = 8
Langsung kita substitusi ke rumus:
P(A) = n(A) / n(S) = 7/8
Lalu, kita cari peluang komplemennya:
P(Ac) = 1 – P(A) = 1 – 7/8 = 8/8 – 7/8 = 1/8 = 0,125
Jadi, peluang tidak muncul gambar satu pun adalah 0,125.
Frekuensi Harapan Suatu Kejadian
Ketika kamu belajar peluang kejadian, jangan bingung kalo kamu nemuin frekuensi harapan. Frekuensi harapan atau disimbolkan dengan Fh(A), bisa juga disebut sebagai ekspektasi suatu kejadian.
Frekuensi harapan pada suatu percobaan adalah hasil kali banyaknya percobaan dengan peluang kejadian secara teoritis. Rumus frekuensi harapan bisa ditulis sebagai berikut:
Contoh
1. Sebuah dadu dilempar 24 kali. Jika A adalah kejadian muncul mata dadu prima ganjil, maka tentukanlah frekuensi harapan munculnya kejadian A!
Pembahasan:
Diketahui dari soal n = 24
Ingat Rumus Frekuensi Harapan:

Nah, karena A adalah mata dadu prima ganjil, maka A={3,5}
atau n(A)= 2.
Untuk S = {1,2,3,4,5,6} maka n(S)= 6
Lanjut, tinggal masukan ke dalam rumus frekuensi harapan.
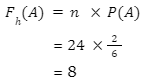
Jadi, frekuensi harapan kejadian A adalah 8.
2. Terdapat 7 buah kartu yang ditulisi huruf A, B, C, D, E, F, G. Lalu, dari kartu tersebut diambil sebuah kartu secara acak. Jika pengambilan dilakukan sebanyak 70 kali dengan pengembalian, maka frekuensi harapan terambil kartu yang bertuliskan huruf vokal adalah…
Pembahasan:
Diketahui:
n(A) = banyaknya huruf vokal yang tersedia yaitu 2 (A dan E)
n(S) = banyaknya kartu yaitu 7
n = banyaknya pengambilan yaitu 70 kali
Maka, frekuensi harapan terambil kartu bertuliskan huruf vokal adalah:
fh(A) = n x P(A)
= n x n(A) / n(S)
= 70 x 2 / 7
= 20
Jadi, frekuensi harapan terambil kartu bertuliskan huruf vokal adalah 20.







Post a Comment