1. Program Linear

Model Matematika Program Linear

Nilai Optimum Fungsi Objektif
Menggunakan garis selidikMembandingkan nilai fungsi objektif tiap titik ekstrimMenggunakan Garis Selidik
Latihan Soal Program Linear dan Pembahasan

Contoh soal dan Pembahasan
2. Barisan dan Deret Aritmetika
Barisan merupakan urutan dari suatu anggota-anggota himpunan berdasarkan suatu aturan tertentu. Misalkan seorang pedagang pada hari pertama jualan memperoleh untung sebesar Rp 10.000,-. Setiap harinya, untung yang diperoleh bertambah sebesar Rp 2000,-. Sehingga untung yang diperoleh pedagang tersebut dapat dituliskan dalam sebuah barisan artimetika berikut:
Rp 10.000, Rp 12.000, Rp 14.000, Rp 16.000, …
Barisan aritmetika merupakan barisan bilangan yang memiliki beda atau selisih tetap antara dua suku yang berurutan.
Contoh Barisan Aritmetika:
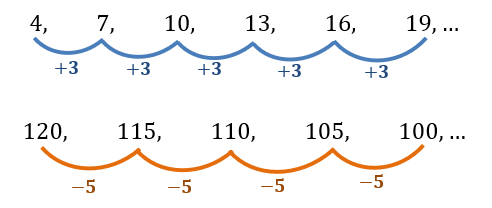
Rumus untuk menentukan suku ke-n dari barisan aritmetika:
Rumus untuk mencari beda pada barisan aritmetika:
Berbeda dengan barisan, deret merupakan hasil penjumlahan pada barisan aritmetika. Namun, deret tidak selalu menjumlahkan keseluruhan suku dalam suatu barisan. Rumus deret hanya menjumlahkan barisan aritmetikanya hanya sampai suku yang diperintahkan saja.
Contoh deret aritmetika:
2 + 4 + 6 + 8 + 10 + …
24 + 20 + 16 + 12 + …
Rumus jumlah n suku pertama deret aritmetika:
Contoh :
Diketahui sebuah barisan aritmetika 15, 19, 23, 27, 31, … .
a. Tentukan suku ke 25!
b. Tentukan 10 suku pertama!
Pembahasan :
Sisipan
Jika hendak membuat sebuah baris aritmatika dengan telah diketahui nilai suku pertama (a) dan suku terakhirnya (p), dapat disisipkan sejumlah bilangan diantara keduan bilangan tersebut. Sejumlah bilangan (q buah) tersebut menjadi suku-suku baris aritmatika dan memiliki selisih antar suku beredekatan (b). Baris aritmatika tersebut memiliki jumah suku q + 2 dan diurut berupa:
a, (a + b), (a + 2b), (a + 3b), …, (a + q.b), (a + (q+1)b)
Diketahui bahwa suku terakhir:
(a + (q+1)b) = p
Maka, nilai b dapat ditentukan sebagai:
Misalkan a= 1 dan p = 9, jika disisipkan 3 bilangan diantara a dan p, maka baris belangan aritmatikanya adalah:
- Nilai q = 3
- Jumlah suku = q + 2 = 3 + 2 = 5
- Baris aritmatika : 1, 3, 5, 7, 9
Suku Tengah
Jika barisan aritmatika memiliki jumlah suku ganjil, maka memiliki suku tengah. Suku tengah baris aritmatika adalah suku ke- . Jika diselesaikan dalam rumus
, maka nilai suku tengah didapatkan:
Barisan dan Deret Geometri
Apakah kamu menyadari bahwa tinggi bola yang memantul semakin lama semakin rendah?
Nah, jika kita mendata tinggi pantulan bola, maka tingginya akan berurutan menjadi semakin rendah dengan rasio yang sama. Misalkan tinggi awal bola dijatuhkan adalah 4 meter, dan pantulan berikutnya adalah ½ dari tinggi sebelumnya, maka barisan geometri yang terbentuk, yaitu
Barisan geometri merupakan barisan bilangan dimana dua suku yang berurutan memiliki perbandingan yang sama. Perbandingan pada barisan geometri disebut sebagai rasio (r).
Contoh barisan geometri:
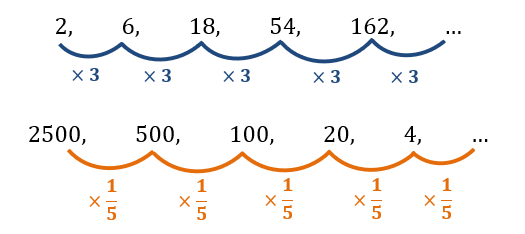
Rumus untuk menentukan suku ke-n dari barisan geometri:
Rumus untuk mencari rasio pada barisan geometri:
Deret geometri merupakan hasil penjumlahan pada barisan geometri. Rumus deret hanya menjumlahkan suku-suku pada barisan geometri hanya sampai suku yang diperintahkan saja.
Contoh deret geometri:
2 + 4 + 8 + 16 + 32 + …
200 + 100 + 50 + 25 + …
Rumus jumlah n suku pertama deret geometri:
Contoh :
Diketahui sebuah barisan geometri berikut:
3, 12, 48, 192, …
a. Tentukan suku ke-10 dari barisan geometri tersebut!
b. Tentukan jumlah 5 suku pertama dari barisan geometri tersebut!
Pembahasan:
Sisipan
Jika hendak membuat sebuah baris geometri dengan telah diketahui nilai suku pertama (a) dan suku terakhirnya (p), dapat disisipkan sejumlah bilangan diantara keduan bilangan tersebut. Sejumlah bilangan (q buah) tersebut menjadi suku-suku baris geometri dan memiliki rasio antar suku beredekatan (r). Baris tersebut memiliki banyak suku q + 2 dan diurutkan menjadi:
a, ar, ar2, ar3, …,arq, ar(q+1)
Dimana suku terakhir tersebut:
ar(q+1) = p
Sehingganilai r dapat ditentukan sebagai:
Deret Geometri Tak hingga
Suatu deret geometri dapat menjumlakan suku-sukunya sampai menuju tak hingga. Apabila deret geometri menuju tak hingga dimana , maka deret ini dapat dijumlah menjadi:
Atau sebagai :
Deret geometri tak hingga terdiri dari 2 jenis yaitu konvergen dan divergen. Deret geometri tak hingga bersifat konvergen jika penjumlahan dari suku-sukunya menuju atau mendekati suatu bilangaan tertentu. Sedangkan bersifat divergen jika penjumlahan dari suku-sukunya tidak terbatas. Nilai deret geometri tak hingga dapat diperoleh dengan mengunakan limit. Sebelumnya diketahui bahwa nilai deret geometri adalah:
Dimana terdapat unsur didalam perhitungannya yang terpengaruh jumlah suku n. Jika
, maka untuk menentukan nilai
dapat menggunakan limit yaitu:
dengan syarat -1 < r < 1.
Dan:
dengan syarat r < -1 atau r > 1.
Kemudian hasil limit tersebut dapat dimasukan kedalam perhitungan deret sebagai:
dengan syarat -1 < r < 1
Dan:
dengan syarat r < -1 atau r > 1.
Contoh Soal Barisan dan Deret Aritmatika/Geometri dan Pembahasan
1. Contoh Soal Deret Aritmatika
Suatu deret aritmatika memiliki suku ke-5 sama dengan 42, dan suku ke-8 sama dengan 15. Jumlah 12 suku pertama deret tersebut adalah?
Pembahasan:
- Diketahui bahwa
,
, maka dapat digunakan rumus :
- Dimana:
- Sehingga:
- Diperoleh:
2. Contoh Soal Deret Geometri
Jika jumlah 2 suku pertama deret geometri adalah 6 dan jumlah 4 suku pertama adalah 54. Memiliki rasio positif. Maka tentukan jumlah 6 suku pertama deret tersebut!
Pembahasan:
- Diketahui bahwa:
dan
- Jika kedua persamaan disubstitusikan :
Dan
- Sehingga :
3. Contoh Soal Geometri Tak Hingga
Jika maka jumlah deret geometri tak hingga
adalah?
Pembahasan 3:
- Diketahui bahwa:
atau
- Ditentukan ratio deretnya adalah:
- Maka jumlah deretnya dengan mensubstitusi
adalah:
Contoh soal dan Pembahasan
Soal Nomor 1
Pembahasan :
Pembahasan :
Pembahasan :
Pembahasan :
Pembahasan :
Dari suatu barisan aritmetika, diketahui suku ketiga adalah 36 dan jumlah suku kelima adalah 144. Jumlah sepuluh suku pertama deret tersebut adalah ….
A. 840
B. 660
C. 640
D. 630
E. 315
Pembahasan :
Diketahui:
Dan
Mencari nilai suku pertama (a) dan beda (b):
Eliminasi a dari persamaan (1) dan persamaan (2):
Substitusi nilai b = 12 pada persamaan (1) untuk mendapatkan nilai a.
Jadi, jumlah sepuluh suku pertama deret tersebut adalah
Jawaban: B
Soal Nomor 7
Sebuah suku ke-5 sebuah deret aritmetika adalah 11 dan jumlah nilai suku ke-8 dengan suku ke-12 sama dengan 52. Jumlah 8 suku yang pertama deret tersebut adalah ….
A. 68
B. 72
C. 76
D. 80
E. 84
Pembahasan :
Diketahui:
Dan,
Eliminasi a dari persamaan (1) dan persamaan (2) untuk medapatkan nilai b.
Substitusi nilai b = 3 pada persamaan (1) untuk mendapatkan nilai a.
Jadi, jumlah 8 suku yang pertama deret tersebut adalah
Jawaban: C
Soal Nomor 8
Suku ketiga suatu barisan aritmetika adalah 154. Jumlah suku kelima dan suku ketujuh adalah 290. Jumlah 10 suku pertama sama dengan ….
A. 3.470
B. 1.735
C. 1.465
D. 1.425
E. 1.375
Pembahasan :
Diketahui:
Dan
Eliminasi a dari persamaan (1) dan persamaan (2) untuk mendapatkan nilai b.
Substitusi nilai b = – 3 untuk mendapatkan nilai a:
Jadi, panjang tali semula adalah
Jawaban: C
Soal Nomor 9
Suku ketiga suatu barisan aritmatika adalah 22. Jika jumlah suku ketujuh dan suku ke sepuluh adalah 0, maka jumlah lima suku pertama sama dengan ….
A. 30
B. 60
C. 85
D. 110
E. 220
Pembahasan :
Diketahui suku ketiga (U3) dan jumlah suku ketujuh (U7) dan suku kesepuluh (U10).
Dan
Eliminasi a dari dua kali persamaan (1) dan persamaan (2) untuk mendapatkan nilai b.
Substitusi nilai b = – 4 pada persamaan (1) untuk mendapatkan nilai a.
Jadi, jumlah lima suku pertama sama dengan
Jawaban: D
Sebuah mobil dibeli dengan harga Rp80.000.000,00. Setiap tahun nilai jualnya menjadi dari harga sebelumnya. Nilai jual setelah dipakai 3 tahun adalah ….
A. Rp20.000.000,00
B. Rp25.312.000,00
C. Rp33.750.000,00
D. Rp35.000.000,00
E. Rp45.000.000,00
Pembahasan :
Berdasarkan informasi dari soal cerita pada soal, dapat diperoleh informasi suku pertama (a) dan rasio (r).
Setelah 3 tahun, nilai jual setelah dipakai 3 tahun adalah
Jawaban: C
Soal Nomor 11
Bakteri jenis A berkembang biak menjadi dua kali lipat setiap lima menit. Pada waktu lima belas menit pertama banyaknya bakteri ada 400. Banyaknya bakteri pada waktu tiga puluh lima menit pertama adalah ….
A. 640 bakteri
B. 3.200 bakteri
C. 6.400 bakteri
D. 12.800 bakteri
E. 32.000 bakteri
Pembahasan :
Berdasarkan soal cerita pada soal dapat diperoleh informasi suku rasio (r) dan suku ketiga (U3).
Mencari nilai suku pertama (a):
Suku ke pada menit ke 35:
Jadi, banyaknya bakteri pada waktu tiga puluh lima menit pertama (U7) adalah
Jawaban: C
Soal Nomor 12
Seutas tali dipotong menjadi 8 bagian yang panjangnya masing-masing membentuk deret geometri. Apabila tali yang paling pendek adalah 3 cm dan yang terpanjang adalah 384 cm, maka panjang tali semula adalah ….
A. 387 cm
B. 465 cm
C. 486 cm
D. 765 cm
E. 768 cm
Pembahasan :
Diketahui deret geometri dengan suku pertama (a = U1) adan suku kedelapan (U8) adalah
Mencari rasio (r):
Jadi, maka panjang tali semula (S8)adalah
Pembahasan: D
Soal Nomor 13
Setiap tahun harga jual tanah di sebuah komplek perumahan mengalami kenaikan 20% dari tahun sebelumnya, sedangkan harga jual bangunannya mengalami penurunan 5% dari tahun sebelumnya. Harga jual sebuah rumah (tanah dan bangunan) saat ini di komplek tersebut apabila 5 tahun yang lalu dibeli seharga 210 juta rupiah dan perbandingan harga jual tanah terhadap bangunan pada saat pertama kali membeli adalah 4 : 3 adalah … juta rupiah.
Pembahasan :
Harga jual bangunan (tanah dan rumah) saat pertama kali membeli adalah Rp210.000.000,00 dengan perbandingan tanah : bangunan = 4 : 3.
Harga tanah saat pertama kali membeli
Harga bangunan saat pertama kali membeli
Harga tanah setiap tahun naik 20%:
Harga bangunan setiap tahun turun 5%:
Jadi, harga jual bangunan (tanah dan rumah) setelah 5 tahun adalah
Jawaban: E













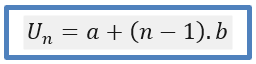


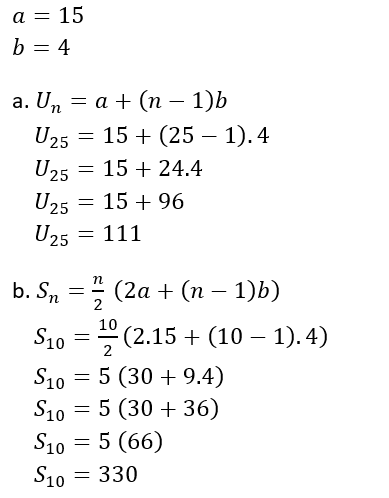
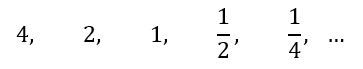
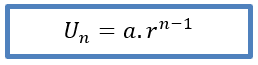


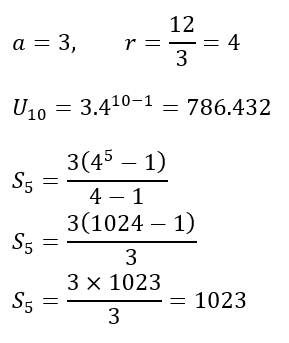

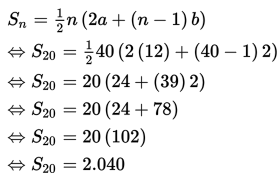
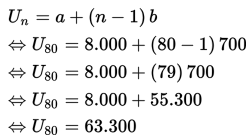

Post a Comment