Barisan dan Deret Aritmetika
Barisan merupakan urutan dari suatu anggota-anggota himpunan berdasarkan suatu aturan tertentu. Misalkan seorang pedagang pada hari pertama jualan memperoleh untung sebesar Rp 10.000,-. Setiap harinya, untung yang diperoleh bertambah sebesar Rp 2000,-. Sehingga untung yang diperoleh pedagang tersebut dapat dituliskan dalam sebuah barisan artimetika berikut:
Rp 10.000, Rp 12.000, Rp 14.000, Rp 16.000, …
Barisan aritmetika merupakan barisan bilangan yang memiliki beda atau selisih tetap antara dua suku yang berurutan.
Contoh Barisan Aritmetika:
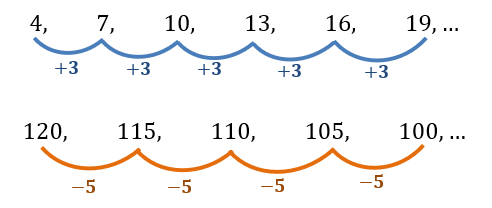
Rumus untuk menentukan suku ke-n dari barisan aritmetika:
Rumus untuk mencari beda pada barisan aritmetika:
Berbeda dengan barisan, deret merupakan hasil penjumlahan pada barisan aritmetika. Namun, deret tidak selalu menjumlahkan keseluruhan suku dalam suatu barisan. Rumus deret hanya menjumlahkan barisan aritmetikanya hanya sampai suku yang diperintahkan saja.
Contoh deret aritmetika:
2 + 4 + 6 + 8 + 10 + …
24 + 20 + 16 + 12 + …
Rumus jumlah n suku pertama deret aritmetika:
Contoh :
Diketahui sebuah barisan aritmetika 15, 19, 23, 27, 31, … .
a. Tentukan suku ke 25!
b. Tentukan 10 suku pertama!
Pembahasan :
Sisipan
Jika hendak membuat sebuah baris aritmatika dengan telah diketahui nilai suku pertama (a) dan suku terakhirnya (p), dapat disisipkan sejumlah bilangan diantara keduan bilangan tersebut. Sejumlah bilangan (q buah) tersebut menjadi suku-suku baris aritmatika dan memiliki selisih antar suku beredekatan (b). Baris aritmatika tersebut memiliki jumah suku q + 2 dan diurut berupa:
a, (a + b), (a + 2b), (a + 3b), …, (a + q.b), (a + (q+1)b)
Diketahui bahwa suku terakhir:
(a + (q+1)b) = p
Maka, nilai b dapat ditentukan sebagai:
Misalkan a= 1 dan p = 9, jika disisipkan 3 bilangan diantara a dan p, maka baris belangan aritmatikanya adalah:
- Nilai q = 3
- Jumlah suku = q + 2 = 3 + 2 = 5
- Baris aritmatika : 1, 3, 5, 7, 9
Suku Tengah
Jika barisan aritmatika memiliki jumlah suku ganjil, maka memiliki suku tengah. Suku tengah baris aritmatika adalah suku ke- . Jika diselesaikan dalam rumus
, maka nilai suku tengah didapatkan:
Barisan dan Deret Geometri
Apakah kamu menyadari bahwa tinggi bola yang memantul semakin lama semakin rendah?
Nah, jika kita mendata tinggi pantulan bola, maka tingginya akan berurutan menjadi semakin rendah dengan rasio yang sama. Misalkan tinggi awal bola dijatuhkan adalah 4 meter, dan pantulan berikutnya adalah ½ dari tinggi sebelumnya, maka barisan geometri yang terbentuk, yaitu
Barisan geometri merupakan barisan bilangan dimana dua suku yang berurutan memiliki perbandingan yang sama. Perbandingan pada barisan geometri disebut sebagai rasio (r).
Contoh barisan geometri:
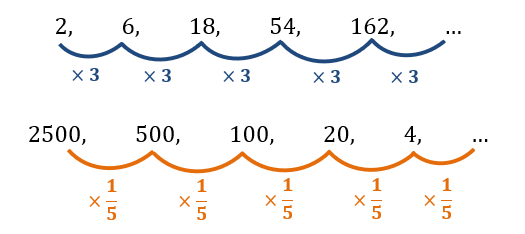
Rumus untuk menentukan suku ke-n dari barisan geometri:
Rumus untuk mencari rasio pada barisan geometri:
Deret geometri merupakan hasil penjumlahan pada barisan geometri. Rumus deret hanya menjumlahkan suku-suku pada barisan geometri hanya sampai suku yang diperintahkan saja.
Contoh deret geometri:
2 + 4 + 8 + 16 + 32 + …
200 + 100 + 50 + 25 + …
Rumus jumlah n suku pertama deret geometri:
Contoh :
Diketahui sebuah barisan geometri berikut:
3, 12, 48, 192, …
a. Tentukan suku ke-10 dari barisan geometri tersebut!
b. Tentukan jumlah 5 suku pertama dari barisan geometri tersebut!
Pembahasan:
Sisipan
Jika hendak membuat sebuah baris geometri dengan telah diketahui nilai suku pertama (a) dan suku terakhirnya (p), dapat disisipkan sejumlah bilangan diantara keduan bilangan tersebut. Sejumlah bilangan (q buah) tersebut menjadi suku-suku baris geometri dan memiliki rasio antar suku beredekatan (r). Baris tersebut memiliki banyak suku q + 2 dan diurutkan menjadi:
a, ar, ar2, ar3, …,arq, ar(q+1)
Dimana suku terakhir tersebut:
ar(q+1) = p
Sehingganilai r dapat ditentukan sebagai:
Deret Geometri Tak hingga
Suatu deret geometri dapat menjumlakan suku-sukunya sampai menuju tak hingga. Apabila deret geometri menuju tak hingga dimana , maka deret ini dapat dijumlah menjadi:
Atau sebagai :
Deret geometri tak hingga terdiri dari 2 jenis yaitu konvergen dan divergen. Deret geometri tak hingga bersifat konvergen jika penjumlahan dari suku-sukunya menuju atau mendekati suatu bilangaan tertentu. Sedangkan bersifat divergen jika penjumlahan dari suku-sukunya tidak terbatas. Nilai deret geometri tak hingga dapat diperoleh dengan mengunakan limit. Sebelumnya diketahui bahwa nilai deret geometri adalah:
Dimana terdapat unsur didalam perhitungannya yang terpengaruh jumlah suku n. Jika
, maka untuk menentukan nilai
dapat menggunakan limit yaitu:
dengan syarat -1 < r < 1.
Dan:
dengan syarat r < -1 atau r > 1.
Kemudian hasil limit tersebut dapat dimasukan kedalam perhitungan deret sebagai:
dengan syarat -1 < r < 1
Dan:
dengan syarat r < -1 atau r > 1.
Contoh Soal Barisan dan Deret Aritmatika/Geometri dan Pembahasan
1. Contoh Soal Deret Aritmatika
Suatu deret aritmatika memiliki suku ke-5 sama dengan 42, dan suku ke-8 sama dengan 15. Jumlah 12 suku pertama deret tersebut adalah?
Pembahasan:
- Diketahui bahwa
,
, maka dapat digunakan rumus :
- Dimana:
- Sehingga:
- Diperoleh:
2. Contoh Soal Deret Geometri
Jika jumlah 2 suku pertama deret geometri adalah 6 dan jumlah 4 suku pertama adalah 54. Memiliki rasio positif. Maka tentukan jumlah 6 suku pertama deret tersebut!
Pembahasan:
- Diketahui bahwa:
dan
- Jika kedua persamaan disubstitusikan :
Dan
- Sehingga :
3. Contoh Soal Geometri Tak Hingga
Jika maka jumlah deret geometri tak hingga
adalah?
Pembahasan 3:
- Diketahui bahwa:
atau
- Ditentukan ratio deretnya adalah:
- Maka jumlah deretnya dengan mensubstitusi
adalah:


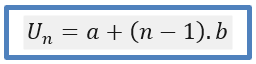


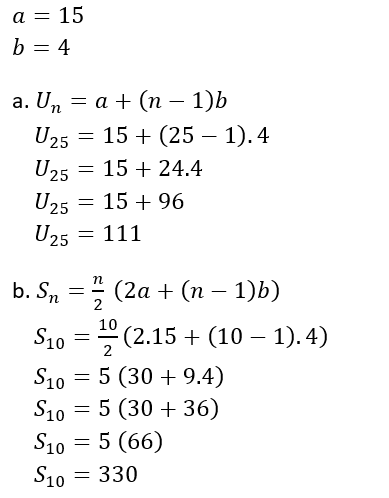
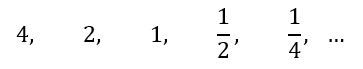
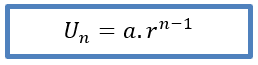


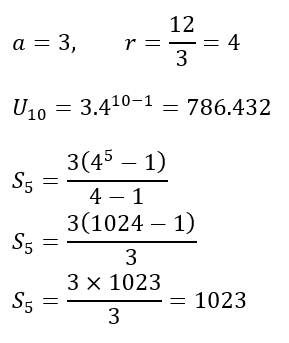




0 Comments