Pada kesempatan Admin akan memposting beberapa soal yang berkaitan dengan materi barisan dan deret. Soal-soal berkaitan dengan masalah dalam kehidupan sehari-hari.
Soal Nomor 1
Pembahasan :
Pembahasan :
Pembahasan :
Pembahasan :
Pembahasan :
Dari suatu barisan aritmetika, diketahui suku ketiga adalah 36 dan jumlah suku kelima adalah 144. Jumlah sepuluh suku pertama deret tersebut adalah ….
A. 840
B. 660
C. 640
D. 630
E. 315
Pembahasan :
Diketahui:
Dan
Mencari nilai suku pertama (a) dan beda (b):
Eliminasi a dari persamaan (1) dan persamaan (2):
Substitusi nilai b = 12 pada persamaan (1) untuk mendapatkan nilai a.
Jadi, jumlah sepuluh suku pertama deret tersebut adalah
Jawaban: B
Soal Nomor 7
Sebuah suku ke-5 sebuah deret aritmetika adalah 11 dan jumlah nilai suku ke-8 dengan suku ke-12 sama dengan 52. Jumlah 8 suku yang pertama deret tersebut adalah ….
A. 68
B. 72
C. 76
D. 80
E. 84
Pembahasan :
Diketahui:
Dan,
Eliminasi a dari persamaan (1) dan persamaan (2) untuk medapatkan nilai b.
Substitusi nilai b = 3 pada persamaan (1) untuk mendapatkan nilai a.
Jadi, jumlah 8 suku yang pertama deret tersebut adalah
Jawaban: C
Soal Nomor 8
Suku ketiga suatu barisan aritmetika adalah 154. Jumlah suku kelima dan suku ketujuh adalah 290. Jumlah 10 suku pertama sama dengan ….
A. 3.470
B. 1.735
C. 1.465
D. 1.425
E. 1.375
Pembahasan :
Diketahui:
Dan
Eliminasi a dari persamaan (1) dan persamaan (2) untuk mendapatkan nilai b.
Substitusi nilai b = – 3 untuk mendapatkan nilai a:
Jadi, panjang tali semula adalah
Jawaban: C
Soal Nomor 9
Suku ketiga suatu barisan aritmatika adalah 22. Jika jumlah suku ketujuh dan suku ke sepuluh adalah 0, maka jumlah lima suku pertama sama dengan ….
A. 30
B. 60
C. 85
D. 110
E. 220
Pembahasan :
Diketahui suku ketiga (U3) dan jumlah suku ketujuh (U7) dan suku kesepuluh (U10).
Dan
Eliminasi a dari dua kali persamaan (1) dan persamaan (2) untuk mendapatkan nilai b.
Substitusi nilai b = – 4 pada persamaan (1) untuk mendapatkan nilai a.
Jadi, jumlah lima suku pertama sama dengan
Jawaban: D
Sebuah mobil dibeli dengan harga Rp80.000.000,00. Setiap tahun nilai jualnya menjadi dari harga sebelumnya. Nilai jual setelah dipakai 3 tahun adalah ….
A. Rp20.000.000,00
B. Rp25.312.000,00
C. Rp33.750.000,00
D. Rp35.000.000,00
E. Rp45.000.000,00
Pembahasan :
Berdasarkan informasi dari soal cerita pada soal, dapat diperoleh informasi suku pertama (a) dan rasio (r).
Setelah 3 tahun, nilai jual setelah dipakai 3 tahun adalah
Jawaban: C
Soal Nomor 11
Bakteri jenis A berkembang biak menjadi dua kali lipat setiap lima menit. Pada waktu lima belas menit pertama banyaknya bakteri ada 400. Banyaknya bakteri pada waktu tiga puluh lima menit pertama adalah ….
A. 640 bakteri
B. 3.200 bakteri
C. 6.400 bakteri
D. 12.800 bakteri
E. 32.000 bakteri
Pembahasan :
Berdasarkan soal cerita pada soal dapat diperoleh informasi suku rasio (r) dan suku ketiga (U3).
Mencari nilai suku pertama (a):
Suku ke pada menit ke 35:
Jadi, banyaknya bakteri pada waktu tiga puluh lima menit pertama (U7) adalah
Jawaban: C
Soal Nomor 12
Seutas tali dipotong menjadi 8 bagian yang panjangnya masing-masing membentuk deret geometri. Apabila tali yang paling pendek adalah 3 cm dan yang terpanjang adalah 384 cm, maka panjang tali semula adalah ….
A. 387 cm
B. 465 cm
C. 486 cm
D. 765 cm
E. 768 cm
Pembahasan :
Diketahui deret geometri dengan suku pertama (a = U1) adan suku kedelapan (U8) adalah
Mencari rasio (r):
Jadi, maka panjang tali semula (S8)adalah
Pembahasan: D
Soal Nomor 13
Setiap tahun harga jual tanah di sebuah komplek perumahan mengalami kenaikan 20% dari tahun sebelumnya, sedangkan harga jual bangunannya mengalami penurunan 5% dari tahun sebelumnya. Harga jual sebuah rumah (tanah dan bangunan) saat ini di komplek tersebut apabila 5 tahun yang lalu dibeli seharga 210 juta rupiah dan perbandingan harga jual tanah terhadap bangunan pada saat pertama kali membeli adalah 4 : 3 adalah … juta rupiah.
Pembahasan :
Harga jual bangunan (tanah dan rumah) saat pertama kali membeli adalah Rp210.000.000,00 dengan perbandingan tanah : bangunan = 4 : 3.
Harga tanah saat pertama kali membeli
Harga bangunan saat pertama kali membeli
Harga tanah setiap tahun naik 20%:
Harga bangunan setiap tahun turun 5%:
Jadi, harga jual bangunan (tanah dan rumah) setelah 5 tahun adalah
Jawaban: E



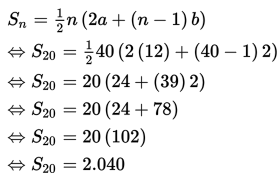
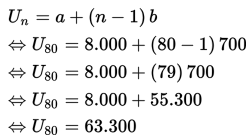

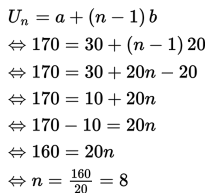
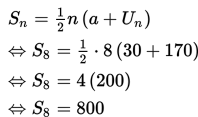
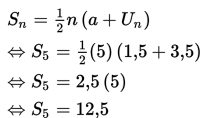
Post a Comment