Ringkasan Materi (Nilai Mutlak, SPLDV)

A. Persamaan dan Pertidaksamaan Nilai Mutlak Linier Satu Variabel

Secara Umum, nilai mutlak x didefinisikan dengan

$$\left|x\right|=\{\begin{array}{c}-xjikax\ge 0\\ -xjikax<0\end{array}$$atau dapat pula ditulis
| x | = -x    jika x ≥ 0
| x | = -x    jika x < 0

Definisi diatas dapat kita maknai sebagai berikut :

Nilai mutlak bilangan positif atau nol adalah bilangan itu sendiri dan nilai mutlak bilangan negatif adalah lawan dari bilangan tersebut.

Sebagai contoh,
| 7 | = 7      | 0 | = 0      | -4 | = -(-4) = 4
Jadi, jelas bahwa nilai mutlak setiap bilangan real akan selalu bernilai positif atau nol.


Persamaan $\sqrt{x^2}=x$ hanya bernilai benar jika x ≥ 0. Untuk x < 0, maka $\sqrt{x^2}=-x$. Dapat kita tulis$$\sqrt{x^2}=\{\begin{array}{c}-xjikax\ge 0\\ -xjikax<0\end{array}$$Jika kita perhatikan, bentuk diatas sama persis dengan definisi nilai mutlak x. Oleh karenanya, pernyataan berikut benar untuk setiap x bilangan real.$$|x|=\sqrt{x^2}$$Jika kedua ruas persamaan diatas kita kuadratkan akan diperoleh$$|x{|}^2=x^2$$

Persamaan terakhir ini merupakan konsep dasar penyelesaian persamaan atau pertidaksamaan nilai mutlak dengan cara menguadratkan kedua ruas. Seperti yang kita lihat, tanda mutlak bisa hilang jika dikuadratkan. Namun, pada artikel ini kita akan lebih fokus pada bentuk linier, baik dari kasus ataupun solusi, tanpa melibatkan bentuk kuadrat.

| x | = a   dengan a > 0

Persamaan | x | = a artinya jarak dari x ke 0 sama dengan a. Perhatikan gambar berikut.

Jarak -a ke 0 sama dengan jarak a ke 0, yaitu a. Pertanyaannya adalah dimana x agar jaraknya ke 0 juga sama dengan a.

Posisi x ditunjukkan oleh titik merah pada gambar diatas, yaitu x = -a atau x = a. Jelas terlihat bahwa jarak dari titik tersebut ke 0 sama dengan a. Jadi, agar jarak x ke nol sama dengan a, haruslah x = -a atau x = a.

| x | < a  untuk a > 0

Pertaksamaan | x | < a, artinya jarak dari x ke 0 kurang dari a. Perhatikan gambar berikut.

Posisi x ditunjukkan oleh ruas garis berwarna merah, yaitu himpunan titik-titik diantara -a dan a yang biasa kita tulis -a < x < a. Jika kita ambil sebarang titik pada interval tersebut, sudah dipastikan jaraknya ke 0 kurang dari a. Jadi, agar jarak x ke 0 kurang dari a, haruslah -a < x < a.

| x | > a  untuk a > 0

Pertaksamaan | x | > a artinya jarak dari x ke 0 lebih dari a. Perhatikan gambar berikut.

Posisi x ditunjukkan oleh ruas garis berwarna merah yaitu x < -a atau x > a. Jika kita ambil sebarang titik pada interval tersebut, sudah dipastikan jaraknya ke 0 lebih dari a. Jadi, agar jarak x ke nol lebih dari a, haruslah x < -a atau x > a.

Secara intuitif, uraian-uraian diatas dapat kita simpulkan sebagai berikut :

SIFAT : Untuk a > 0 berlaku
a.  | x | = a  ⇔  x = a  atau  x = -a
b.  | x | < a  ⇔  -a < x < a
c.  | x | > a  ⇔  x < -a  atau  x > a

Contoh 1
Tentukan himpunan penyelesaian dari |2x - 7| = 3

Jawab :
Berdasarkan sifat a :
|2x - 7| = 3  ⇔  2x - 7 = 3  atau  2x - 7 = -3
|2x - 7| = 3  ⇔  2x = 10  atau  2x = 4
|2x - 7| = 3  ⇔  x = 5  atau  x = 2

Jadi, HP = {2, 5}.


Contoh 2
Tentukan HP dari |2x - 1| = |x + 4|

Jawab :
Berdasarkan sifat a :
|2x - 1| = |x + 4|

⇔  2x - 1 = x + 4  atau  2x - 1 = -(x + 4)
⇔  x = 5  atau  3x = -3
⇔  x = 5  atau  x = -1

Jadi, HP = {-1, 5}.


Contoh 3
Tentukan himpunan penyelesaian dari |2x - 1| < 7

Jawab :
Berdasarkan sifat b :
|2x - 1| < 7  ⇔  -7 < 2x - 1 < 7
|2x - 1| < 7  ⇔  -6 < 2x < 8
|2x - 1| < 7  ⇔  -3 < x < 4

Jadi, HP = {-3 < x < 4}.


Contoh 4
Tentukan himpunan penyelesaian dari |4x + 2| ≥ 6

Jawab :
Berdasarkan sifat c :
|4x + 2| ≥ 6  ⇔  4x + 2 ≤ -6  atau  4x + 2 ≥ 6
|4x + 2| ≥ 6  ⇔  4x ≤ -8  atau  4x ≥ 4
|4x + 2| ≥ 6  ⇔  x ≤ -2  atau  x ≥ 1

Jadi, HP = {x ≤ -2  atau  x ≥ 1}.

Dalam menyelesaikan persamaan dan pertaksamaan nilai mutlak bentuk linier dengan menggunakan definisi, akan sangat membantu jika bentuk |ax + b| kita jabarkan menjadi

|ax + b| = ax + b       jika x ≥ -b/a

|ax + b| = -(ax + b)   jika x < -b/a

Untuk langkah-langkah penyelesaiannya dapat disimak pada contoh-contoh berikut.

Contoh 5
Jabarkan bentuk nilai mutlak berikut :
a.  |4x - 3|
b.  |2x + 8|

Jawab :
a.  Untuk |4x - 3|
     |4x - 3| = 4x - 3       jika  x ≥ 3/4
     |4x - 3| = -(4x - 3)   jika  x < 3/4

b.  Untuk  |2x + 8|
     |2x + 8| = 2x + 8       jika  x ≥ -4
     |2x + 8| = -(2x + 8)   jika  x < -4


Contoh 6
Nilai x yang memenuhi persamaan |x - 2| = 2x + 1 adalah...

Jawab :
|x - 2| = x - 2       jika  x ≥ 2
|x - 2| = -(x - 2)   jika  x < 2

Untuk x ≥ 2
|x - 2| = 2x + 1  ⇔  x - 2 = 2x + 1
|x - 2| = 2x + 1  ⇔  -x = 3
|x - 2| = 2x + 1  ⇔  x = -3
Karena x ≥ 2, maka x = -3 tidak memenuhi

Untuk x < 2
|x - 2| = 2x + 1  ⇔  -(x - 2) = 2x + 1
|x - 2| = 2x + 1  ⇔  -x + 2 = 2x + 1
|x - 2| = 2x + 1  ⇔  -3x = -1
|x - 2| = 2x + 1  ⇔  x = 1/3
Karena x < 2, maka x = 1/3 memenuhi.

Jadi, nilai x yang memenuhi persamaan diatas adalah x = 1/3.


Contoh 7
Tentukan HP dari |x + 1| > 2x - 4

Jawab :
|x + 1| = x + 1       jika  x ≥ -1
|x + 1| = -(x + 1)   jika  x < -1

Untuk x ≥ -1
|x + 1| > 2x - 4  ⇔  x + 1 > 2x - 4
|x + 1| > 2x - 4  ⇔  -x > -5
|x + 1| > 2x - 4  ⇔  x < 5
Irisan dari x ≥ -1 dan x < 5 adalah -1 ≤ x < 5   

Untuk x < -1
|x + 1| > 2x - 4  ⇔  -(x + 1) > 2x - 4
|x + 1| > 2x - 4  ⇔  -x - 1 > 2x - 4
|x + 1| > 2x - 4  ⇔  -3x > -3
|x + 1| > 2x - 4  ⇔  x < 1
Irisan dari x < -1 dan x < 1 adalah x < -1   

Jadi, HP = {x < -1  atau  -1 ≤ x < 5}
Jadi, HP = {x < 5}


Contoh 8
Nyatakan |x - 4| + |2x + 6| tanpa menggunakan simbol nilai mutlak

Jawab :
|x - 4| = x - 4 jika x ≥ 4
|x - 4| = -(x - 4) jika x < 4

|2x + 6| = 2x + 6 jika x ≥ -3
|2x + 6| = -(2x + 6) jika x < -3

Jika interval-interval diatas digambarkan pada garis bilangan akan diperoleh

Untuk x < -3
|x - 4| + |2x + 6| = -(x - 4) - (2x + 6)
|x - 4| + |2x + 6| = -x + 4 - 2x - 6
|x - 4| + |2x + 6| = -3x - 2

Untuk -3 ≤ x < 4
|x - 4| + |2x + 6| = -(x - 4) + (2x + 6)
|x - 4| + |2x + 6| = -x + 4 + 2x + 6
|x - 4| + |2x + 6| = x + 10

Untuk x ≥ 4
|x - 4| + |2x + 6| = (x - 4) + (2x + 6)
|x - 4| + |2x + 6| = x - 4 + 2x + 6
|x - 4| + |2x + 6| = 3x + 2

Dari uraian diatas, kita simpulkan
$|x-4|+|2x+6|=\{\begin{array}{c}-3x-2jikax<-3\\ -x+10jika-3\le x<4\\ -3x+2jikax\ge 4\end{array}$


Contoh 9
Tentukan nilai-nilai x yang memenuhi persamaan
|x + 1| + |2x - 4| = 9

Jawab :
|x + 1| = x + 1       jika  x ≥ -1
|x + 1| = -(x + 1)   jika  x < -1

|2x - 4| = 2x - 4       jika  x ≥ 2
|2x - 4| = -(2x - 4)   jika  x < 2

Untuk x < -1
|x + 1| + |2x - 4| = 9  ⇔  -(x + 1) - (2x - 4) = 9
|x + 1| + |2x - 4| = 9  ⇔  -x - 1 - 2x + 4 = 9
|x + 1| + |2x - 4| = 9  ⇔  -3x = 6
|x + 1| + |2x - 4| = 9  ⇔  x = -2
karena x < -1, maka x = -2 memenuhi.

Untuk -1 ≤ x < 2
|x + 1| + |2x - 4| = 9  ⇔  (x + 1) - (2x - 4) = 9
|x + 1| + |2x - 4| = 9  ⇔  x + 1 - 2x + 4 = 9
|x + 1| + |2x - 4| = 9  ⇔  -x = 4
|x + 1| + |2x - 4| = 9  ⇔  x = -4
karena -1 ≤ x < 2, maka x = -4 tidak memenuhi.

Untuk x ≥ 2 
|x + 1| + |2x - 4| = 9  ⇔  (x + 1) + (2x - 4) = 9
|x + 1| + |2x - 4| = 9  ⇔  x + 1 + 2x - 4 = 9
|x + 1| + |2x - 4| = 9  ⇔  3x = 12
|x + 1| + |2x - 4| = 9  ⇔  x = 4
karena x ≥ 2, maka x = 4 memenuhi.

Jadi, nilai-nilai x yang memenuhi persamaan diatas adalah x = -2  atau  x = 4.


Contoh 10
Tentukan HP dari |x - 1| + |x + 2| ≥ 4

Jawab :
|x - 1| = x - 1       jika  x ≥ 1
|x - 1| = -(x - 1)   jika  x < 1

|x + 2| = x + 2       jika  x ≥ -2
|x + 2| = -(x + 2)   jika  x < -2

Untuk x < -2 
|x - 1| + |x + 2| ≥ 4  ⇔  -(x - 1) - (x + 2) ≥ 4
|x - 1| + |x + 2| ≥ 4  ⇔  -x + 1 - x - 2  ≥ 4
|x - 1| + |x + 2| ≥ 4  ⇔  -2x ≥ 5
|x - 1| + |x + 2| ≥ 4  ⇔  x ≤ -5/2
Irisan dari x < -2 dan x ≤ -5/2 adalah x ≤ -5/2

Untuk -2 ≤ x < 1
|x - 1| + |x + 2| ≥ 4  ⇔  -(x - 1) + (x + 2) ≥ 4
|x - 1| + |x + 2| ≥ 4  ⇔  -x + 1 + x + 2 ≥ 4
|x - 1| + |x + 2| ≥ 4  ⇔  3 ≥ 4  (bukan penyelesaian)

Untuk x ≥ 1 
|x - 1| + |x + 2| ≥ 4  ⇔  (x - 1) + (x + 2) ≥ 4
|x - 1| + |x + 2| ≥ 4  ⇔  2x ≥ 3
|x - 1| + |x + 2| ≥ 4  ⇔  x ≥ 3/2
Irisan dari x ≥ 1 dan x ≥ 3/2 adalah x ≥ 3/2

Jadi, HP = {x ≤ -5/2  atau  x ≥ 3/2}


Contoh 11
Dengan menggunakan definisi nilai mutlak, tunjukkan bahwa untuk setiap x bilangan real dengan a > 0 berlaku | x | < a  ⇔  -a < x < a.

Jawab :
Untuk x ≥ 0 maka | x | = x, akibatnya
| x | < a  ⇔  x < a
Karena a > 0, nilai x yang memenuhi adalah
0 ≤ x < a

Jadi, untuk x ≥ 0 dan a > 0 berlaku
| x | < a  ⇔  0 ≤ x < a   .................................(1)

Untuk x < 0 maka | x | = -x, akibatnya
| x | < a  ⇔  -x < a
| x | < a  ⇔  x > -a
Karena a > 0, nilai x yang memenuhi adalah
  -a < x < 0

Jadi, untuk x < 0 dan a > 0 berlaku
| x | < a  ⇔  -a < x < 0   ................................(2)

Dari (1) dan (2) kita simpulkan
Untuk setiap x bilangan real dan a > 0 berlaku
| x | < a  ⇔  -a < x < 0  atau  0 ≤ x < a
| x | < a  ⇔  -a < x < a

B. Sistem Persamaan Linear Dua Variabel (SPLDV)

Sistem Persamaan Linear Dua Variabel atau yang biasa disebut dengan SPLDV adalah dua persamaan linear dua variabel yang memiliki hubungan diantara keduanya dan memiliki satu penyelesaian.

Berikut ini adalah bentuk umum dari sistem persamn linear dua variabel:

ax + by = c

px + qy = r

Ket:

• x dan y adalah variabel
• a, b, p, dan q adalah koefisien
• c dan r adalah konstanta

Cara Menyelesaikan Persamaan Linear Dua Variabel (SPLDV)

Metode Eliminasi

Dengan menggunakan metode Eliminasi, kita harus mengeliminasi/menghilangkan salah satu variabel dengan cara penjumlahan ataupun pengurangan. Untuk lebih jelasnya perhatikan contoh berikut.

Tentukan himpunan selesaian dari SPLDV yang memuat persamaan-persamaan

2x + 5y = –3 dan 3x – 2y = 5.

Grafik dari kedua persamaan tersebut dapat digambarkan sebagai berikut.

     

Untuk menentukan selesaiannya, pertama kita harus mengeliminasi salah satu variabelnya. Misalkan kita akan mengeliminasi variabel x, maka kita harus menyamakan koefisien x dari kedua persamaan tersebut. Koefisien x pada persamaan 1 dan 2 secara berturut-turut adalah 2 dan 3. Sehingga kita harus menyamakan koefisien x dari kedua persamaan tersebut menjadi KPK dari 2 dan 3, yaitu 6, dengan mengalikan persamaan 1 dengan 3 dan persamaan 2 dengan 2.

     

   

Sehingga diperoleh selesaiannya adalah x = 1 dan y = –1, atau dapat dituliskan sebagai himpunan selesaian Hp = {(1, –1)}.

Metode Campuran 

Metode eliminasi juga dapat dipadukan dengan metode substitusi dalam menyelesaikan suatu permasalahan SPLDV. Perhatikan contoh berikut. Selisih umur seorang ayah dan anak perempuannya adalah 26 tahun, sedangkan lima tahun yang lalu jumlah umur keduanya 34 tahun. Hitunglah umur ayah dan anak perempuannya dua tahun yang akan datang.Misalkan umur ayah dan anak perempuannya secara berturut-turut adalah m dan n, maka permasalahan di atas dapat dimodelkan sebagai berikut.

Grafik dari persamaan-persamaan m – n = 26 dan m + n = 44 dapat digambarkan seperti berikut.

Pertama, kita akan mengeliminasi variabel n untuk mendapatkan nilai dari m dengan menjumlahkan persamaan 1 dengan persamaan 2.

    

Selanjutnya kita substitusikan m = 35 ke salah satu persamaan, misalkan ke persamaan 1. Sehingga diperoleh,

Jadi, umur ayah dan anak perempuannya saat ini secara berturut-turut adalah 35 tahun dan 9 tahun.

Metode Subsitusi

Metode subsitusi adalah suatu metode yang digunakan khusus untuk menyelesaiakan suatu persamaan linear dua variabel dengan menggunakan metode subsitusi. Disini Anda harus menggunakan cara dengan menyebutkan lebih dahulu variabel yang satu ke dalam variabel lainya dari sebuah persamaan. Selanjutnya tinggal menggantikan atau menyubtitusikan variabel itu ke dalam persamaan lainnya.

Contoh:

Untuk lebih memahami dalam menyelesaikan permasalahan SPLDV dengan

metode substitusi, perhatikan contoh berikut.

Selisih uang Samuel dan Andini adalah Rp 3.000,00. Jika 2 kali uang Samuel ditambah dengan 3 kali uang Andini adalah Rp 66.000,00. Tentukanlah besarnya uang masing-masing.

Langkah pertama, kita modelkan informasi yang ada di soal menjadi persamaan-

persamaan matematika. Misalkan s dan a secara berturut-turut merupakan banyaknya uang Samuel dan Andini. Karena selisih uang Samuel dan Andini adalah Rp 3.000,00, maka kalimat tersebut dapat diubah menjadi persamaan sebagai berikut.

Selain itu, jumlah dari dua kali uang Samuel dan tiga kali uang Andini adalah Rp 66.000,00, maka

Sehingga, pada langkah pertama ini kita menghasilkan persamaan 1 dan 2 yang masing-masing dinyatakan dalam variabel s dan a.

Langkah kedua, kita akan menyatakan variabel s pada persamaan 1 ke dalam

variabel a.

Langkah ketiga, substitusikan persamaan 3 ke dalam persamaan 2 untuk mendapatkan nilai dari a.

Langkah keempat, tentukan nilai variabel s dengan mensubstitusi nilai a yang diperoleh ke dalam persamaan 3.

Langkah kelima, tentukan selesaian dari SPLDV yang diberikan dan jawablah pertanyaan yang diberikan soal. Dari langkah 4 dan 5, kita memperoleh selesaian dari SPLDV tersebut adalah s = 15.000 dan a = 12.000. Sehingga, banyaknya uang Samuel adalah Rp 15.000,00 dan banyaknya uang Andini adalah Rp 12.000,00.

Metode Grafik

Pada pembahasan ini akan dibahas bagaimana cara menyelesaikan SPLDV dengan menggunakan metode grafik. Tetapi, sebelum itu kita harus tahu bentuk grafik dari persamaan linear dua variabel. Bagaimana bentuk grafik dari persamaan linear dua variabel?

Grafik dari persamaan linear dua variabel berbentuk garis lurus, seperti yang

ditunjukkan oleh gambar berikut.

Lalu bagaimana cara menggunakan grafik persamaan linear untuk menyelesaikan

permasalahan SPLDV? Pada dasarnya, terdapat 4 langkah dalam menyelesaiakan permasalahan SPLDV dengan menggunakan metode grafik. Keempat langkah tersebut adalah,

Langkah 1: Memodelkan informasi yang ada di soal.

Langkah 2: Menentukan dua titik yang dilalui grafik persamaan-persamaan pada SPLDV 

Langkah 3: Menggambar grafik persamaan-persamaan tersebut.

Langkah 4: Menggunakan penyelesaian yang diperoleh untuk menjawab pertanyaan pada soal cerita.

Untuk lebih memahaminya, perhatikan contoh berikut.

Dalam sebuah konser musik, terjual karcis kelas I dan kelas II sebanyak 500 lembar. Harga karcis kelas I adalah Rp 8.000,00, sedangkan harga karcis kelas II adalah Rp 6.000,00. Jika hasil penjualan seluruh karcis adalah Rp 3.250.000,00, tentukan banyak karcis masing-masing kelas I dan kelas II yang terjual.

Langkah pertama adalah mengubah kalimat-kalimat pada soal cerita di atas

menjadi model matematika, sehingga membentuk sistem persamaan linear. Misalkan banyak karcis I dan II yang terjual secara berturut-turut adalah x dan y, maka kalimat “Dalam sebuah konser musik, terjual karcis kelas I dan kelas II sebanyak 500 lembar,” dapat dimodelkan menjadi,

       Sedangkan kalimat, “Harga karcis kelas I adalah Rp 8.000,00, sedangkan harga karcis            kelas II adalah Rp 6.000,00. Jika hasil penjualan seluruh karcis adalah Rp 3.250.000,00,”         dapat dimodelkan menjadi

Sehingga diperoleh SPLDV sebagai berikut.

Langkah kedua, kita cari koordinat dua titik yang dilewati oleh grafik masing- masing persamaan tersebut. Biasanya, dua titik yang dipilih tersebut merupakan titik potong grafik persamaan-persamaan tersebut dengan sumbu-x dan sumbu-y.

Sehingga grafik persamaan x + y = 500 memotong sumbu-x di (500, 0) dan memotong sumbu-y di (0, 500).

Sedangkan grafik 8.000x + 6.000y = 3.250.000 memotong sumbu-x di (406 1/4, 0) dan memotong sumbu-y di (0, 541 2/3).

Langkah ketiga, kita gambarkan grafik persamaan-persamaan tersebut pada

        koordinat Cartesius. Grafik persamaan-persamaan di atas dapat dilukis dengan memplot         titik-titik yang telah         kita cari pada koordinat Cartesius kemudian hubungkan titik                (500, 0) dan (0, 500) untuk mendapatkan grafik x + y = 500, serta titik (406 1/4, 0) dan             (0, 541 2/3) untuk mendapatkan grafik 8.000x + 6.000y = 3.250.000.

Dari grafik di atas diperoleh bahwa titik potong grafik x + y = 500 dan 8.000x + 6.000y = 3.250.000 adalah (125, 375). Sehingga selesaian dari SPLDV di atas adalah x = 125 dan y = 375.

Langkah keempat, kita gunakan selesaian di atas untuk menjawab pertanyaan

pada soal cerita. Karena x dan y secara berturut-turut menyatakan banyak karcis I dan II yang terjual, maka banyaknya karcis kelas I yang terjual adalah 125 lembar dan 375 lembar untuk karcis kelas II

Berikut ini adalah permasalah dalam sistem persaman linear dua variabel:

• Persamaan yang pertama: 2x + 3y = 8
• Persamaan yang kedua: 3x + y = 5

Penyelesaian sistem persamaan linear dua variabel dengan menggunakan metode grafik.

Langkah pertama adalah menggambar kedua grafik

Menentukan titik potong pada kedua sumbu x dan juga y dari kedua persamaan itu sendiri.

Reperesentasi kedua persaman dalam bidang kartesius.

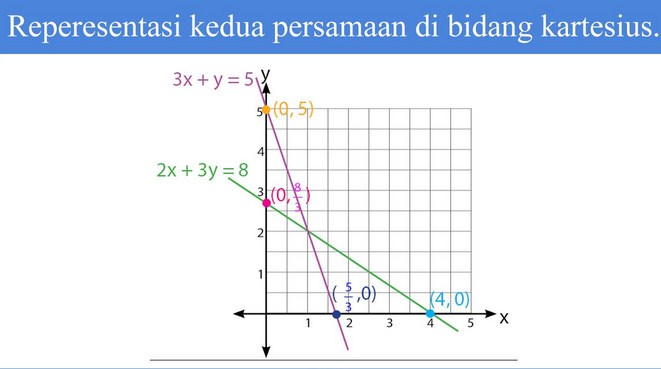
Langkah kedua adalah menemukan titik potong dari kedua grafik itu sendiri.

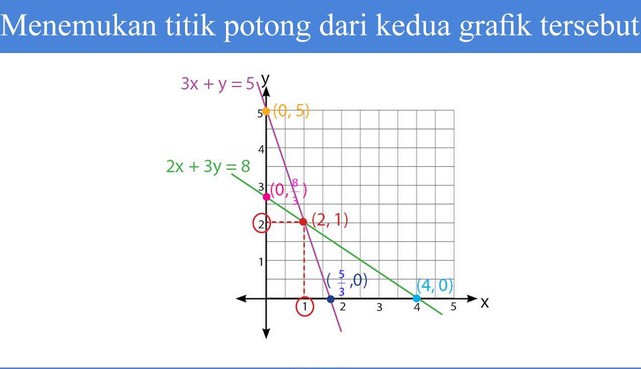
Langkah ketiga yang dimana penyelesaiannya adalah (x, y)

Berdasarkan gambar diatas maka dapat diketahui bahwa titik potong berada pada x = 1 dan juga y = 2

Jadi daerah penyelesaiannya adalah (1,2).

Contoh Soal Persamaan Linear Dua Variabel

Untuk lebih jelasnya, berikut ini kami akan memberikan beberapa contoh soal cerita dan soal yang sudah pasti pernah ada di UN. Berikut ini ulasan selengkapnya.