Pada kesempatan kali ini kami akan memposting artikel tentang "Soal dan Pembahasan Bentuk Akar". Semoga beberapa contoh di bawah ini dapat membantu anda menyelesaikan soal-soal yang terkait dengan bentuk akar.
Contoh 1
√75 + 2√12 - √27 = . . . . .
A. 2√3
B. 3√3
C. 4√3
D. 5√3
E. 6√3
B. 3√3
C. 4√3
D. 5√3
E. 6√3
Pembahasan:
√75 + 2√12 - √27 = √(25x3) + 2√(4x3) - √(9x3)
= (√25 x √3) + 2 x (√4 x √3) - (√9 x √3)
= 5√3 + 4√4 - 3√3
= (5+4-3)√3
= 6√3 -------> Jawaban: E
Contoh 2
(√7 + √2)(√7 - √2) = . . . . ..
A. 2
B. 5
C. 7
D. 2√7
E. 2√2
B. 5
C. 7
D. 2√7
E. 2√2
Pembahasan:
(√7 + √2)(√7 - √2) = √7.√7 - √7.√2 + √7.√2 - √2.√2
= 7 - √14 + √14 - 2
= 7 - 0 - 2
= 5 -----------> Jawaban: B
Contoh 3
Jika a = (5 + √50), b = (2 + √18) dan c = (7 - √32) maka bentuk paling sederhana dari (a + b - c) adalah. . . . .
A. 6
B. 2√2
C. √2
D. 4√2
E. 12√2
B. 2√2
C. √2
D. 4√2
E. 12√2
Pembahasan:
a + b - c = (5 + √50) + (2 + √18) - (7 - √32)
= 5+ √50 + 2 + √18 - 7 + √32
= 5 + 2 - 7+ √50 + √18 + √32
= 0+ √(25x2) + √(9x2) + √(16x2)
= (√25 x √2)+ (√9 x √2) + (√16 x √2)
= 5√2 + 3√2 + 4√2
= 12√2
Contoh 4
Bentuk
sama dengan . . . . .
A. 13(4+ √3)
B. 13(4 - √3)
C. 13/7 (4+ √3)
D. (4+ √3)
E. (4 - √3)
Pembahasan:
= 5
= 5 + 2 - 7
= 0
= (√25 x √2)
= 5√2 + 3√2 + 4√2
= 12√2
Contoh 4
Bentuk
A. 13(4
B. 13(4 - √3)
C. 13/7 (4
D. (4
E. (4 - √3)
Pembahasan:
=
=
= (4
Contoh 5
Jika penyebut pecahan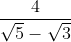 
dirasionalkan, maka bentuknya ekuivalen dengan . . . .
A. 2√5+ √3
B. 2√5 + 2√3
C. 2√5 - √3
D. 2√5 - 2√3
E. 2√2
Pembahasan:
A. 2√5
B. 2√5 + 2√3
C. 2√5 - √3
D. 2√5 - 2√3
E. 2√2
Pembahasan:
=
= 2(√5
= 2√5 + 2√3 ------> Jawaban: B
Contoh 6
Dengan merasionalkan penyebut dari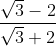
, bentuk sederhananya adalah...
A. -7 - 4√3
B. -7 + 4√3
C. -1 + (4/7)√3
D. 1 - (4/7)√3
E. 1 + 4√3
Pembahasan:
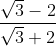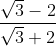= x 
=
=
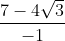
= -7 + 4√3 ----> Jawaban: B
Dengan merasionalkan penyebut dari
A. -7 - 4√3
B. -7 + 4√3
C. -1 + (4/7)√3
D. 1 - (4/7)√3
E. 1 + 4√3
Pembahasan:
=
=
= -7 + 4√3 ----> Jawaban: B