Menentukan Turunan Fungsi Aljabar

 

Turunan fungsi aljabar merupakan pembahasan lebih jauh dari limit fungsi. Dengan kata lain turunan fungsi merupakan fungsi tertentu dimana nilai fungsi di setiiap titik ditentukan dengan batas selisih fungsi. Secara umum dijelaskan sebagai berikut. Jika dipunyai fungsi f(x) dan turunan f'(x), kedua fungsi tersebut memiliki hubungan:

Jika dipunyai fungsi f(x) fungsi aljabar diperoleh dasar turunan sebagai berikut.

1. f(x) = x n , maka f '(x) = nx n-1

2. f(x) = ax n , maka f '(x) = anx n-1 Sifat-sifat turunan fungsi aljabar Jika diketahui k suatu konstanta, u = u(x), v = v(x) dan masing-masing memiliki turunan u'(x) dan v'(x), maka berlaku: 1. f(x) = u + v, maka f'(x) = u' + v' 2. f(x)= u - v , maka f'(x) = u' - v' 3. f(x) = uv, maka f'(x) = u'v + uv' 4. f(x) = f(u), maka f' (x) = f'(u). u' 5. f(x) = u/v, maka f'(x) = (u'v - uv')/ v 2 Untuk lebih jelasnya perhatikan beberapa contoh berikut. Contoh 1 Tentukan turunan fungsi-fungsi berikut.

1.    f(x) = x 3 + x 2

2.    f(x) = 4x 2 + 5x

3.    f(x) = 3x 5 + 4x 3 – 7x 2

4.    f(x) = 2x 4 + 8x 3 – x 2 – 9x + 1

5.    f(x) = x 7 + 2x 5 – 6x 4 – 9x 2 + 11x

jawaban :

1.    f' (x) = 3x 3-1 + 2x 2-1

             = 3x2 + 2x

2.    f'(x) = 4.2x 2-1 + 5x 1-1

             = 8x + 5

3.    f' (x) = 3,5x 5-1 + 4,3x 3-1 – 7,2x 2-1

             =15x 4 + 12x 2 – 14x

4.    f' (x) = 2,4x 4-1 + 8,3x 3-1 – 2x 2-1 – 9

             = 8x 3 + 24x 2 – 2x – 9

5.    f'(x) = 7.x 7-1 + 2.5x 5-1 – 6.4x 4-1 – 9.2x 2-1 + 11x 1-1

        = 7x 6 + 10x 4 – 24x 3 – 18x + 11

Contoh 2 

Tentukan turunan fungsi berikut.

1.        F(x) = (x + 2)(2x 3 – 5)

2.        F(x) = (x 2 + 5)(4x 3 – 3x)

3.        F(x) = (x + 2)/(3x – 4)

4.        F(x) = (x 2 + 1)/(x 2 – 1)

jawaban :

1.      F(x) = (x + 2)(2x 3 – 5)

Misalkan u = x + 2,     maka u' = 1

dan  v = 2x 3 – 5, maka v' = 6x 2

f'(x) = u'v + uv'

       =1 . (2x 3 – 5) + (x + 2) . 6x 2

       = 2x 3 – 5 + 6x 3 + 12x 2

       = 8x 3 + 12x 2 – 5

2.      F(x) = (x 2 + 5)(4x 3 – 3x)

Misalkan u = x 2 + 5,     maka u' = 2x

dan  v = 4x 3 – 3x, maka v' = 12x 2 – 3

f'(x) = u'v + uv'

       = 2x . (4x 3 – 3x) + (x 2 + 5).(12x 2 – 3)

       = (8x 4 – 6x 2 ) + (12x 4 – 3x 2 – 15)

       = 20x 4 – 9x 2 – 15

3.      F(x) = (x + 2)/(3x – 4)

Misalkan u = x + 5,     maka u' = 1

dan  v = 3x – 4, maka v' = 3

      

      

4.   F(x) = (x 2 + 1)/(x 2 – 1)

      Misalkan u = x 2 + 1,     maka u' = 2x

      dan  v = x 2 – 1, maka v' = 2x

Contoh 3
Tentukan turunan fungsi berikut.

1.    F(x) = (2x + 3) 5

2.    F(x) = (3x 2 – 2) 4

3.    F(x) = (x 3 + 2x) 5

 jawaban :

1.    F(x) = (2x + 3) 5

Misal u = 2x + 3, sehingga du/dx = u' = 2

Y = f(x) = u 5   Sehingga dy/du = 5u 4

F'(x) = dy/du    .   du/dx

        = 5u 4   .   2

        = 10u 4

        =10 (2x + 3 ) 4

2.    F(x) = (3x 2 – 2) 4

Misal u = 3x 2 – 4, sehingga du/dx = u' = 6x

Y = f(x) = u 4   Sehingga dy/du = 4u 3

F'(x) = dy/du    .   du/dx

        = 4u 3   .   6x

        = 24xu 3

        =24(3x 2 – 4) 3

3.    F(x) = (x 3 + 2x) 5

Misal u = x 3 + 2x, sehingga du/dx = u' = 3x 2 + 2

Y = f(x) = u 5   Sehingga dy/du = 5u 4

F'(x) = dy/du    .   du/dx

        = 5u 4   .   (3x 2 + 2)

        = 5(x 3 + 2x) 4 . (3x 2 + 2)

Sebuah produk massal biasanya dibuat melalui beberapa proses. Proses-proses tersebut ditangani oleh mesin-mesin yang berbeda. Urutan pengerjaan produk tersebut tentu tidak boleh tertukar. Sebagai contoh, pada sebuah pabriksirop, mesin pencuci buah digunakan terlebih dahulu sebelum mesin pengupas buah digunakan. Begitu seterusnya hingga sirop dikemas.

Prinsip yang sama berlaku pada komposisi fungsi. Dalam bahasa yang mudah, komposisi fungsi adalah operasi penyusunan beberapa fungsi dengan aturan tertentu sehingga terbentuk fungsi baru. Urutan penggabungan fungsi akan berpengaruh terhadap komposisi fungsi yang dihasiikan. Sebagai catatan, jika hasii komposisi fungsi berupa fungsi, hasil komposisi fungsi itu disebut fungsi komposisi.

• Fungsi Injektif (Fungsi Satu-Satu)
  Fungsi f dari A ke B merupakan fungsi injektif jika anggota B dipasangkan dengan tepat ke satu anggota A, tetapi tidak semua anggota B harus mempunyai pasangan dengan anggota A. Dengan kata lain, fungsi f dari A ke B merupakan fungsi injektif jika a1 , a2 € Df dengan a1 ≠ a2 maka f(a1) ≠ f(a2). Df = daerah asal fungsi f.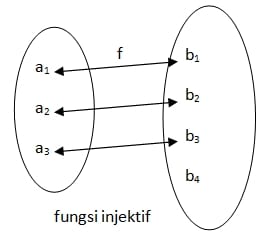
  

• Fungsi surjektif (Fungsi onto)
  Fungsi f dari A ke B merupakan fungsi surjektif jika setiap anggota B mempunyai pasangan dengan anggota A.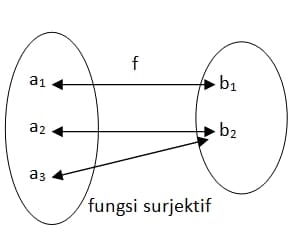
  

• Fungsi Bijektif (Fungsi Berkorespondensi Satu-Satu)
  Suatu fungsi dikatakan bijektif jika fungsi tersebut merupakan fungsi injektif sekaligus surjektif.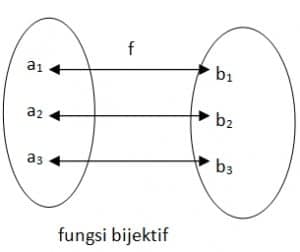
  

Aljabar Fungsi

1. Penjumlahan, Pengurangan, Perkalian, dan Pembagian Dua Fungsi

Jika f dan g merupakan fungsi, berlaku sifat-sifat aijabar fungsi sebagai berikut.

1. Penjumlahan fungsi : (f + g)(x) = f(x) + g(x)
2. Pengurangan fungsi: (f – g)(x) = f(x) – g(x)
3. Perkalian fungsi : (f . g)(x) = f(x) . g(x)
4. Pembagian fungsi : (f/g) (x) = f(x)/g(x) . g(x) ≠ 0

2. Daerah Asal Fungsi

Diketahui f dan g merupakan fungsi dengan Df = daerah asal f dan Dg = daerah asal g. Daerah asal operasi aljabar dua fungsi sebagai berikut.

1. Daerah asal fungsi (f + g)(x): Df + g = Df ∩ Dg
2. Daerah asal fungsi (f – g)(x): Df -g = Df ∩ Dg
3. Daerah asal fungsi (f . g)(x) : Df.g = Df ∩ Dg
4. Daerah asal fungsi (f/g) (x) : Df/g = Df ∩ Dg dengan g(x)  0

Komposisi Fungsi

1. Pengertian Komposisi Fungsi

Jika f dan g merupakan fungsi, komposisi fungsi f dan g (ditulis f ₒ g) dirumuskan sebagai berikut.

(f ₒ g)(x) = f(g(x))

 f ₒ g dibaca f bundaran g atau f komposisi g.
Artinya, mula-mula unsure x € Dg dipetakan oleh g ke g(x), kemudian g(x) dipetakan oleh f ke f(g(x)). Dengan cara yang sama diperoleh komposisi fungsi berikut.

(g ₒ f)(x) = g(f(x))
(f ₒ g ₒ h)(x) = f(g(h(x)))

2. Sifat-Sifat Komposisi Fungsi

1. Komposisi fungsi tidak bersifat komutatif.
   (f ₒ g)(x) ≠ (g ₒ f)(x)
2. Komposisi fungsi bersifat asosiatif.
   (f ₒ g ₒ h)(x) – (f ₒ (g ₒ h))(x) = ((f ₒ g) ₒ h)(x)
3. Dalam komposisi fungsi terdapat sebuah fungsi identitas, yaitu |(x) = x sehingga (f ₒ l)(x) = (I ₒ f)(x) = f(x)