Definisi Pola Bilangan Menurut Para Ahli
- Menurut Walle (2002) pola bilangan meliputi pola berulang dan pola berkembang. Pada pola berkembang memiliki komponen numeris, yaitu jumlah objek setiap langkah (Walle, 2002) yang memungkinkan kita menemukan angka pada pola kesekian atau jumlah objek pada langkah kesekian.
- Menurut Aksin (2017) pola bilangan dapat diartikan sebagai susunan bilangan yang memiliki keteraturan.
- Menurut Kemdikbud (2017) pola barisan adalah bilangan-bilangan yang disusun berturut dengan aturan tertentu.
Macam Macam Pola Bilangan
Berikut ini jenis pola bilangan dalam matematika dan contohnya:
Pola Bilangan Ganjil
Pengertian pola bilangan ganjil adalah pola bilangan yang terbentuk dari bilangan-bilangan ganjil. Sedangkan pengertian bilangan ganjil adalah suatu bilangan asli yang tidak habis dibagi dua ataupun kelipatannya.Pola bilangan ganjil adalah 1, 3, 5, 7,……..
Gambar Pola Bilangan Ganjil
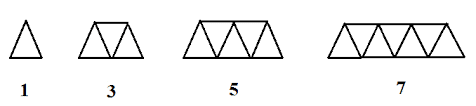
Rumus Pola Bilangan ganjil
1 , 3 , 5 , 7 , . . . , n , maka rumus pola bilangan ganjil ke n adalah: Un = 2n – 1
Keterangan:
n = bilangan asli atau urutan bilangan yang ingin dicari (ke-n)
Pola Bilangan Genap
Kalau tadi udah yang ganjil, sekarang yang genap nih. Kalau yang ini susunan bilangan yang habis dibagi 2. Contoh bilangannya adalah 2, 4, 6, 8, 10, dan seterusnya. Coba dihitung deh bilangan-bilangan tadi habis nggak kalau dibagi 2. Seperti ini rumusnya:
Un = 2n
Keterangan:
n : urutan bilangan ke-n
Pola Bilangan Aritmatika
Pola bilangan aritmatika adalah bilangan yang susunannya memiliki selisih tetap antar kedua sukunya. Jadi angka tambahnya selalu sama ya. Contoh bilangannya seperti pada kasus pedagang kue di awal tadi, yaitu 8, 16, 24, 48, dan seterusnya (a = 8, b = 8). Ini dia rumusnya:
Pola Bilangan Aritmatika
Pola bilangan aritmatika adalah bilangan yang susunannya memiliki selisih tetap antar kedua sukunya. Jadi angka tambahnya selalu sama ya. Contoh bilangannya seperti pada kasus pedagang kue di awal tadi, yaitu 8, 16, 24, 48, dan seterusnya (a = 8, b = 8). Ini dia rumusnya:
Pola Bilangan Geometri
Pola bilangan geometri adalah susunan bilangan yang membentuk pola dengan rasio selalu tetap antar kedua sukunya. Nah loh, gimana tuh? Rasio tuh apa sih? Kalau bingung langsung aja lihat contoh bilangannya yaitu 2, 6, 18, 54, dan seterusnya. Dari susunan bilangan tersebut, kira-kira rumusnya bagaimana ya? Rumusnya adalah:
Un = arn-1
Keterangan:
a : suku pertama dari susunan bilangan
r : rasio
n : urutan bilangan ke-n
Pola Bilangan Persegi
Pola bilangan persegi adalah susunan bilangan yang polanya seperti persegi, sehingga dibentuk oleh bilangan kuadrat. Rumus pola bilangan persegi yaitu Un = n2. Contoh susunan bilangannya adalah 1, 4, 9, 16, dan seterusnya.
Pola Bilangan Persegi Panjang
Hampir sama seperti sebelumnya, tapi rumusnya berbeda jauh lho, guys. Kalau ini akan menghasilkan bentuk menyerupai bangun datar persegi panjang. Contoh susunan angkanya adalah 2, 6, 12, 20, dan seterusnya.
Coba deh elo bikin gambar bilangan persegi panjang dari contoh susunan angkanya. Kalau dituliskan dalam bentuk rumus akan seperti ini:
Un = n (n+1)
Pola Bilangan Segitiga
Dari namanya, kita udah bisa langsung menebak kalau pola bilangan segitiga ini akan membentuk bangun segitiga, betul atau betul? Nah, segitiga yang dimaksud di sini adalah bentuk segitiga sama sisi. Coba perhatikan gambar di bawah ini:
Bener kan, bilangannya jadi membentuk pola segitiga. Kamu bisa cirikan suatu kelompok bilangan yang polanya seperti ini, bisa dikatakan bahwa bilangan tersebut membentuk pola segitiga. Contohnya adalah bilangan 1, 3, 6, 10, 15, dan seterusnya. Cek rumus pola bilangan segitiga di bawah ini ya:
Un = ½ n (n+1)
Pola Bilangan Fibonacci
Kok yang satu ini namanya aneh sendiri? Ternyata pola bilangan Fibonacci adalah susunan bilangan yang berawalan 0 dan 1, kemudian angka berikutnya diperoleh dengan cara menambahkan kedua bilangan sebelumnya secara berturut-turut.
Contoh bilangannya adalah 0, 1, 1, 2, 3, 5, 8, 13, 21, dan seterusnya. Seperti ini aturan dan ilustrasinya:
Supaya lebih mudah, kamu bisa gunakan rumus berikut ini:
Un = (n – 1) + (n – 2)
Pola Bilangan Pascal
Terakhir, ada yang namanya pola bilangan Pascal. Mungkin beberapa dari kamu udah nggak asing dengan nama Pascal ya. Yap, ditemukan oleh Blaise Pascal, seorang ilmuwan asal Prancis. Lebih dikenal sebagai segitiga Pascal.
Lalu, apa hubungannya dengan pola bilangan? Segitiga Pascal merupakan suatu pola bilangan. Kamu bisa melihatnya dari berbagai peraturan atau ketentuannya di sini:
- Baris paling atas ditulis satu kotak saja, yaitu 1.
- Setiap baris dalam segitiga pascal selalu diawali dan akan diakhiri oleh angka 1.
- Jumlah kotak selanjutnya dalam segitiga pascal ini ditulis di baris ke-2 sampai ke-n adalah hasil penjumlahan dua bilangan diagonal di atasnya.
- Setiap baris akan membentuk simetris.
- Banyak bilangan di setiap barisnya memiliki kelipatan dua dari jumlah angka baris sebelumnya.
Sangat unik, bukan? Supaya lebih terbayang, kamu bisa lihat gambar berikut ini ya.





Post a Comment