Nilai Fungsi Trigonometri Sudut Istimewa

Nilai fungsi trigonometri dari sebuah sudut bisa diperoleh dengan cara menggunakan kalkulator, tabel trigonometri, atau dari perbandingan segitiga siku-siku. Khusus untuk sudut tertentu, nilainya bisa didapatkan dengan mudah tanpa menggunakan kalkulator. Sudut-sudut ini dinamakan sudut istimewa. Dikatakan demikian karena berasal dari segitiga istimewa.

Nilai fungsi trigonometri sudut istimewa disarankan untuk dipahami dan dihapalkan karena selalu muncul pada pokok bahasan yang berkaitan dengan trigonometri.

Terdapat lima jenis sudut istimewa yang diperoleh dari segitiga istimewa. Kelima sudut tersebut adalah 0°, 30°, 45°, 60°, dan 90°. Untuk sudut 30°, 45°, dan 60° nilainya bisa diperoleh dari perbandingan segitiga siku-siku istimewa. Ada dua jenis segitiga siku-siku istimewa, yaitu segitiga 30-60 (dua sudut selain sudut siku-siku besarnya 30° dan 60°) serta segitiga 45 (dua sudut selain sudut siku-siku masing-masing sebesar 45°).

Berikut ini Nilai fungsi trigonometri sudut istimewa yang diperoleh dari segitiga siku-siku istimewa.

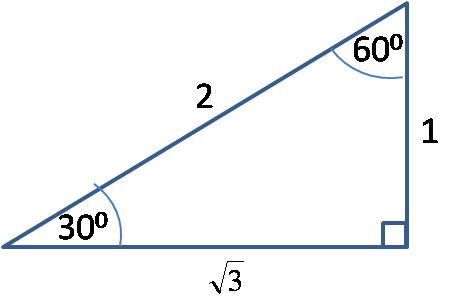
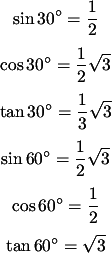
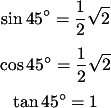
Nilai fungsi trigonometri untuk 0° dan 90° adalah sebagai berikut (silakan pikirkan dari mana nilai tersebut didapat?).

sin 0°=0
cos 0°=1
tan 0°=0
sin 90°=1
cos 90°=0
tan 90°=∞

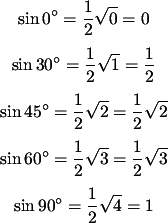
Agar lebih mudah menghapalkannya, Kamu bisa gunakan cara berikut ini. Pikirkan bilangan 0-4 kemudian akarkan lalu kalikan dengan 1/2. Nilainya berturut-turut merupakan nilai sinus sudut istimewa.

* 0-4 merupakan pola bilangan di dalam akar.

Sedangkan untuk menghapal nilai cosinus sudut istimewa adalah dengan cara membalik urutan nilai fungsi sinus. Pikirkan bilangan 4,3,2,1,0 kemudian akarkan lalu kalikan dengan 1/2. Nilainya berturut-turut seperti berikut ini.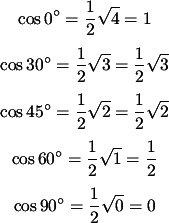

* Perhatikan juga urutan sudut-sudut istimewanya.

Untuk mendapatkan nilai tangen, cukup dengan membagi nilai sinus oleh cosinus untuk sudut yang sesuai. Ingat bahwa .

Berikut nilai-nilai trigonometri sudut istimewa disajikan dalam sebuah tabel.

Fungsi	Sudut
Fungsi	0°	30°	45°	60°	90°
sin	0				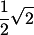1
cos	1				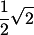0
tan	0		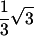1		∞

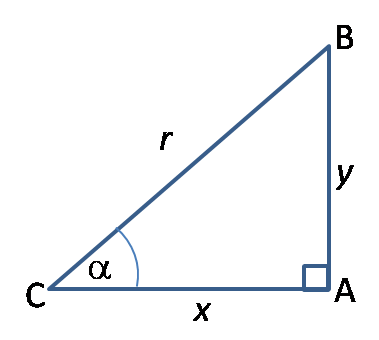
Identitas Trigonometri (Identitas Pythagoras)

Segitiga di samping merupakan segitiga siku-siku. Jenis segitiga tersebut sudah dikenal sejak Sekolah Dasar. Teorema Pythagoras yang melekat pada jenis segitiga tersebut juga terkenal. Saya masih inget waktu SD, ada poster dipampang di kelas bertuliskan Teorema Pythagoras. Cuma sekadar baca aja waktu itu tanpa ngerti apa maksudnya. Pokok bahasan mengenai Teorema Pythagoras mulai dipelajari sejak kelas VIII SMP. Ternyata Teorema Pythagoras ini berguna dalam menyelesaikan permasalahan geometri, trigonometri, dan sebagainya. Kali ini Saya akan menjelaskan Identitas Trigonometri yang diperoleh dari Teorema Pythagoras. Identitas ini disebut juga sebagai Identitas Pythagoras. Dinamakan demikian mungkin karena diperoleh dari Teorema Pythagoras. Oke, langsung aja.Menurut Teorema Pythagoras, sisi-sisi pada segitiga di atas memenuhi hubungan sebagai berikut.

x²+y²=r²

Agar diperoleh suatu bentuk perbandingan trigonometri, Kita bagi dengan sebuah sisi, misalnya dengan sisi r.

Dari persamaan yang terakhir ini muncul pecahan yang merupakan pembagian satu sisi segitiga dengan sisi yang lainnya. Menurut perbandingan trigonometri, bentuk pembagian tersebut menjadi seperti berikut ini.

cos²α+sin²α=1

⇔ sin²α+cos²α=1

Inilah salah satu identitas trigonometri yang menunjukkan hubungan antara sinus dan cosinus. Identitas trigonometri yang lainnya bisa didapatkan dengan membagi persamaan dari Teorema Pythagoras oleh sisi yang lainnya, misalnya oleh sisi x.

Apabila dibagi oleh sisi y,

Berikut ini identitas trigonometri yang diperoleh dari Teorema Pythagoras (Identitas Pythagoras).

sin²α+cos²α=1

1+tan²α=sec²α

1+cot²α=csc²α

Contoh soal dan pembahasan

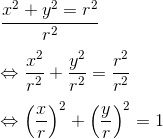
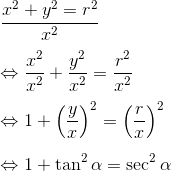
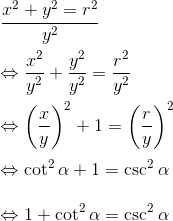
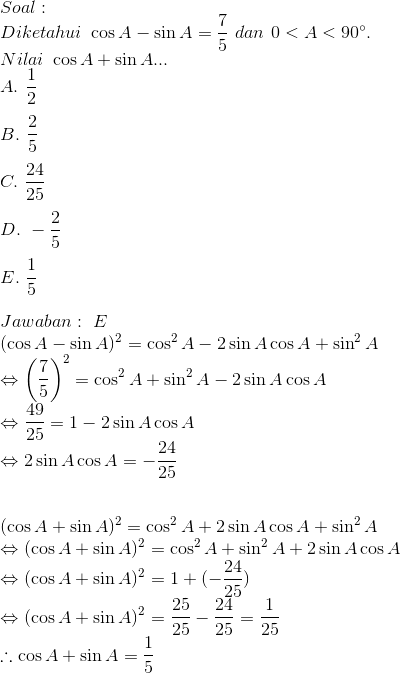
Grafik Fungsi Trigonometri

Secara umum, grafik fungsi trigonometri dibagi menjadi tiga, yaitu sebagai berikut.

1. Grafik fungsi sinus (y = a sin bx, x ∈ [0^o, 360^o])

Grafik fungsi sinus, y = a sin bx, x ∈ [0^o, 360^o] memiliki bentuk gelombang bergerak yang teratur seiring pergerakan x. Perhatikan gambar berikut.

Berdasarkan grafik di atas, diperoleh sifat-sifat berikut.

Simpangan maksimum gelombang atau yang biasa disebut amplitudo adalah 1. Simpangan gelombang adalah jarak dari fungsi x ke puncak gelombang.
Gelombang memiliki periode satu putaran penuh.
Grafik y = sin x memiliki nilai y_maks = 1 dan y_min = -1.
Titik maksimum gelombang adalah adalah (90^o, 1) dan titik minimumnya (270^o, -1).

Jika persamaan fungsi trigonometrinya diubah menjadi y = a sin x dengan a = 2, diperoleh grafik berikut.

Perubahan nilai a mengakibatkan perubahan amplitudo gelombang. Nah, jika persamaan fungsinya diubah menjadi y = sin bx dengan b = 2, grafiknya akan menjadi seperti berikut.

Artinya, perubahan nilai b mempengaruhi jumlah gelombang yang terbentuk. Pada grafik fungsi y = sin 2x terbentuk 2 buah gelombang.

Untuk memudahkan belajarmu, inilah SUPER “Solusi Quipper”.

2. Grafik fungsi kosinus (y = cos 2x, x ∈ [0^o, 360^o])

Pada dasarnya, grafik fungsi kosinus sama dengan grafik fungsi sinus. Hal yang membedakan adalah grafik fungsi sinus dimulai dari y = 0, sedangkan grafik fungsi kosinus dimulai dari y = 1. Perhatikan grafik berikut.

Jika persamaan fungsinya diubah menjadi y = cos 2x, grafiknya menjadi seperti berikut.

Grafik di atas menujukkan adanya dua buah gelombang yang bergerak dari y = 1.

3. Grafik fungsi tangen (y = tan x, x ∈ [0^o, 360^o])

Adapun ketentuan yang berlaku pada fungsi tangen adalah sebagai berikut.

Saat x -> 90^o dan x -> 270^o (dari kanan), nilai y = tan x menuju tak terhingga.
Saat x -> 90^o dan x -> 270^o (dari kiri), nilai y = tan x menuju negatif tak terhingga.

Berikut ini contoh grafiknya.

Jika fungsi tangen diubah menjadi y = tan 2x, x ∈ [0^o, 360^o] grafiknya menjadi seperti berikut.

Untuk mengasah pemahamanmu tentang grafik fungsi trigonometri, simak contoh soal berikut.

Contoh Soal 1

Perhatikan grafik fungsi berikut.

Grafik fungsi tersebut merupakan grafik fungsi jenis apa?

Pembahasan:

Jika diperhatikan, grafik tersebut dimulai dari titik (0,1) dan mempunyai periode satu putaran 0 ≤ x ≤ 2π.

Dengan demikian, grafik fungsi tersebut adalah grafik fungsi cos, yaitu y = cos x. Untuk meyakinkan, coba lihat salah satu titiknya.

Jadi, grafik fungsi tersebut merupakan grafik fungsi y = cos x untuk 0 ≤ x ≤ 2π.

Contoh Soal 2

Lukislah grafik fungsi y = 2 cos 2x, x ∈ [0^o, 360^o]

Pembahasan:

Untuk menentukan bentuk grafiknya, gunakan tabel trigonometri sudut istimewa.

Dengan demikian, grafik fungsi y = 2 cos 2x, x ∈ [0^o, 360^o] adalah sebagai berikut.

Contoh Soal 3

Hitunglah nilai maksimum dan minimum fungsi y = cos (x – 30), x ∈ [0^o, 360^o]. Kemudian, lukislah grafik fungsinya.

Pembahasan:

Berdasarkan tabel trigonometri untuk sudut istimewa, diperoleh:

Berdasarkan tabel di atas, nilai maksimum dari fungsi y = cos (x – 30), x ∈ [0^o, 360^o] adalah 1 dan nilai minimumnya adalah –1. Untuk lebih jelasnya, simak grafik fungsi berikut.

Aturan Sinus dan Cosinus: Rumus & Contoh Soal

Aturan Sinus

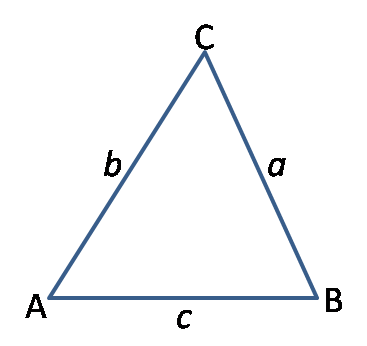
Aturan sinus berbunyi bahwa perbandingan panjang sisi sebuah segitiga dengan sinus sudut yang menghadapnya memiliki nilai yang sama.

Lebih jelasnya pada gambar dibawah ini

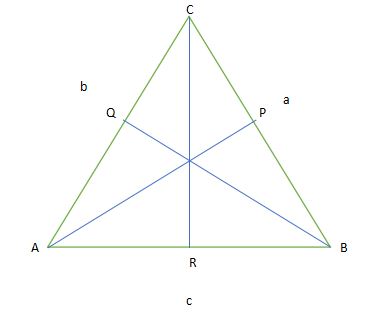
Keterangan

A = besar sudut di hadapan sisi a
a = panjang sisi a
B = besar sudut di hadapan sisi b
b = panjang sisi b
C = besar sudut di hadapan sisi c
c = panjang sisi c
AP ┴ BC
BQ ┴ AC
CR ┴ AB

Perhatikan segitiga ACR

Sin A = CR/b maka CR = b sin A …(1)

Perhatikan segitiga BCR

Sin B = CR/a maka CR = a sin B …. (2)

Perhatikan segitiga ABP

Sin B = AP/c maka AP = c sin B … (3)

Perhatikan segitiga APC

Sin C = AP/b maka AP = b sin C …(4)

Berdasarkan persamaan (1) dan (2) didapat

CR = b sin A = a sin B maka a/sin A = b/sin B …(5)

Berdasarkan persamaan (3) dan (4) didapat

AP = c sin B = b sin C maka b/sin B = c/sin C …(6)

Kemudian, berdasarkan persamaan (5) dan (6) diperoleh

a/sin A = b/sin B = c/sin C

Persamaan ini yang kemudian disebut dengan aturan sinus.

Contoh Soal Aturan Sinus

1. Andi sedang mengukur mainan segitiganya yang tiap sudutnya dikodekan dengan A, B, dan C, kemudian diketahui segitiga tersebut memiliki sudut A = 30º, sisi a = 6cm dan sisi b = 8cm. Hitung besar sudut B!

Pembahasan

Akan dicari besar sudut B

sin B = (b sin A)/a

sin B = 8/6 sin 30̊

sin B = 2/3

B = arc sin B

B = arc sin (2/3)

B = 41,8̊

Jadi, besar sudut B adalah 41,8̊ atau 180̊ – 41,8̊ = 138,2̊

2. Sebuah segitiga ABC memiliki panjang AC = 4 cm. Jika besar ∠ ABC = 60o dan ∠BAC = 30o, maka panjang BC = … cm.

Pembahasan

AC/sin ∠ABC = BC/sin∠BAC

4cm/sin 60 = BC/sin30

4cm/½√3 = BC/½

BC = ½ × 4cm/½√3

BC = 4cm/√3

BC = 4/3 √3 cm

Jadi, panjang BC adalah BC4/3 √3cm.

Aturan Cosinus

Aturan cosinus menjelaskan hubungan antara kuadrat panjang sisi dengan nilai cosinus dari salah satu sudut pada segitiga.

Lebih jelasnya pada gambar dibawah ini.

Keterangan

A = besar sudut di hadapan sisi a
a = panjang sisi a
B = besar sudut di hadapan sisi b
b = panjang sisi b
C = besar sudut di hadapan sisi c
c = panjang sisi c
AP ┴ BC
BQ ┴ AC
CR ┴ AB

Perhatikan segitiga BCR

Sin B = CR/a maka CR = a sin B

Cos B = BR/a maka BR = a cos B

AR = AB – BR = c – a cos B

Perhatikan segitiga ACR

b2 = AR2 + CR2

b2 = (c – a cos B)2 + (a sin B)2

b2 = c2 – 2ac cos B + a2 cos2 B + a2 sin2 B

b2 = c2 – 2ac cos B + a2 (cos2 B + sin2 B)

b2 = c2 + a2– 2ac cos B

Menggunakan analogi yang sama, kemudian diperoleh aturan cosinus untuk segitiga ABC sebagai berikut

a2 = c2 + b2– 2bc cos A

b2 = a2+ c2 – 2ac cos B

c2 = a2+ b2 – 2ab cos C

Contoh Soal Aturan Cosinus

Diketahui sebuah segitiga ABC memiliki sisi dengan panjang

a = 10 cm

c = 12 cm

besar sudut B = 60̊.

Hitung panjang sisi b!

Pembahasan

b2 = a2+ c2 – 2ac cos B

b2 = 100+144 – 44 cos 60̊

b2 = 244 – 44(0,5)

b2 = 244 – 22

b2 = 222

b = 14,8997

Jadi, panjang sisi b adalah 14,8997 cm

Penggunaan Trigonometri dalam Menentukan Luas Segitiga

Diketahui Alas dan Tinggi Segitiga

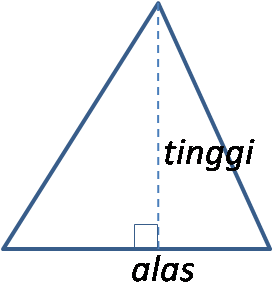
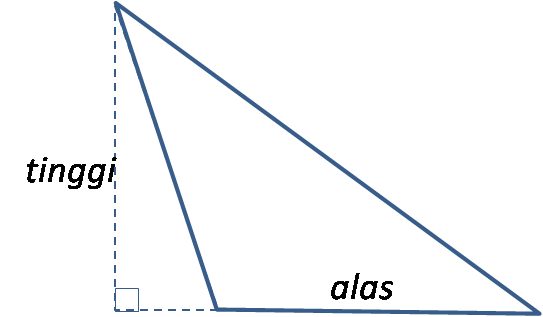
Rumus luas untuk segitiga yang diketahui alas dan tingginya adalah sebagai berikut. LΔ=1/2(alas)(tinggi). Rumus tersebut berlaku untuk semua jenis segitiga. Baik segitiga lancip, tumpul, atapu pun siku-siku. Berikut ini alas dan tinggi untuk segitiga lancip, tumpul, dan siku-siku.

Segitiga Lancip

Segitiga Tumpul

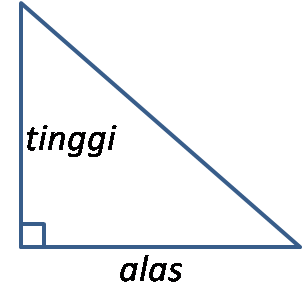
Segitiga Siku-Siku

Luas Segitiga yang Diketahui Dua Sisi dan Sudut yang Diapitnya

Segitiga yang diketahui panjang dua sisi dan sudut yang diapitnya.

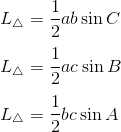
Rumus di atas didasarkan pada rumus luas segitiga yang diketahui alas dan tingginya. Coba perhatikan segitiga di bawah ini.

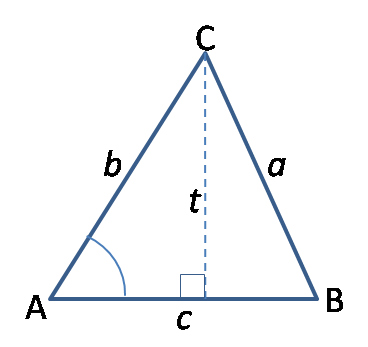
Segitiga yang diketahui panjang dua sisi dan sudut yang diapitnya.

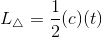
Jika t tidak diketahui, kita bisa mendapatkannya dengan menggunakan perbandingan trigonometri.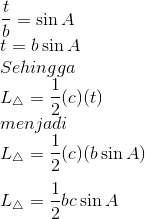

Rumus yang lainnya bisa didapat dengan cara yang sama untuk sisi-sudut-sisi yang berbeda.

Luas Segitiga yang Diketahui Dua Sudut dan Satu Sisi Diketahui

Segitiga yang diketahui panjang dua sudut dan satu sisi.

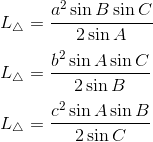
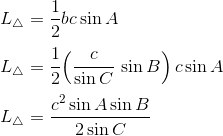
Rumus di atas didapat dari rumus luas segitiga yang diketahui dua sisi dan sudut yang diapitnya salah satu sisinya diubah menjadi rumus aturan sinus.

Luas Segitiga yang Diketahui Ketiga Sisinya

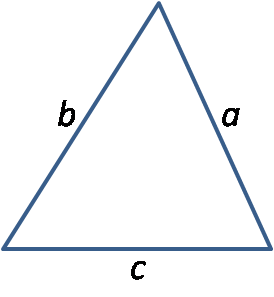
Segitiga yang diketahui panjang ketiga sisinya.

Rumus luas segitiga di atas adalah sebagai berikut.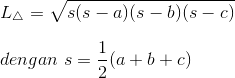

Pembuktiannya silakan sebagai latihan.

Konsep luas segitiga ini sering dipakai juga dalam luas segibanyak beraturan. Luas segi-n beraturan yang diketahui jari-jari lingkaran luarnya=r adalah sebagai berikut.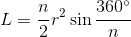

Contoh soal
Tentukan luas segitiga ABC jika diketahui panjang sisi-sisinya adalah a=2, b=3, dan c=4

Jawaban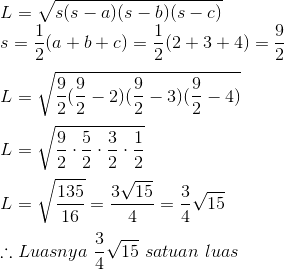

Rumus penjumlahan dan pengurangan fungsi sinus dan cosinus pertama yang akan dibahas adalah rumus sin jumlah. Rumus sin jumlah digunakan ketika sudut hasil jumlah atau selisihnya merupakan sudut istimewa. Contohnya adalah dua sudut tidak istimewa seperti $75^{o}$ dan $15^{o}$ . Hasil jumlah sudut $75^{o}$ dan $15^{o}$ adalah $90^{o}$ , sedangkan selisihnya adalah $60^{o}$ . Keduanya (jumlah dan selisih sudut) merupakan sudut istimewa. Dengan demikian, sobat dapat memanfaatkan rumus penjumlahan dan pengurangan fungsi sinus dan cosinus untuk menyelesaikan soal.

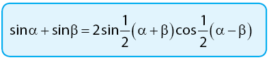
Rumus Penjumlahan Fungsi Sin

Meskipun rumusnya terlihat panjang, namun cara yang dapat digunakan untuk menghafal rumusnya. Cara menghafal rumus sin jumlah dapat menggunakan kalimat: sin jumlah sama dengan dua sin setengah jumlah cos setengah selisih. Simak dari mana rumus di atas diperoleh melalui pembuktian rumus berikut.

Bukti:

Pada pembahasan rumus perkalian fungsi sinus dan cosinus, sudah terbukti bahwa:

$sin \; \left( A + B \right) + sin \; \left( A - B \right) = 2 \ cdot sin \; A \cdot cos \; B$

Misalkan:

$\alpha = A + B$

$\beta = A - B$

Sehingga,

$\alpha + \beta = 2A \rightarrow A = \frac{1}{2}\left( \alpha + \beta \right)$

dan

$\alpha - \beta = 2B \rightarrow B = \frac{1}{2}\left( \alpha - \beta \right)$

Substitusi nilai A, B, $\alpha$ , dan $\beta$ pada rumus perkalian sinus dan cosinus, sehingga,

$sin \; \alpha + sin \; \beta \; = 2 \cdot sin \; \frac{1}{2}\left( \alpha + \beta \right) \cdot cos \; \frac{1}{2}\left( \alpha - \beta \right)$

Terbukti! Berikutnya akan diberikan contoh soal dan pembahasan rumus sin jumlah.

Contoh soal dan pembahasan rumus sin jumlah.
Diketahui besar sudut $\alpha = 105^{o}$ dan $\beta = 15^{o}$ . Nilai $sin \; 105^{o} \; + \; sin \; 15^{o}$ adalah ….

$\textrm{A.} \; \; \; \frac{\sqrt{2}}{6}$

$\textrm{B.} \; \; \; \frac{\sqrt{2}}{2}$

$\textrm{C.} \; \; \; \frac{\sqrt{3}}{6}$

$\textrm{D.} \; \; \; \frac{\sqrt{5}}{2}$

$\textrm{E.} \; \; \; \frac{\sqrt{6}}{2}$

Pembahasan:

$sin \; 105^{o} \; + \; sin \; 15^{o} = 2 \; sin \frac{1}{2} \left( 105^{o} + 15^{o} \right) \; cos \frac{1}{2} \left(105^{o} - 15^{o} \right)$

$sin \; 105^{o} \; + \; sin \; 15^{o} = 2 \; sin \frac{1}{2} \left( 120^{o} \right) \; cos \frac{1}{2} \left(90^{o} \right)$

$sin \; 105^{o} \; + \; sin \; 15^{o} = 2 \; sin \; 60^{o} \; cos \; 45^{o}$

$sin \; 105^{o} \; + \; sin \; 15^{o} = 2 \cdot \frac{1}{2} \sqrt{3} \cdot \frac{1}{2} \sqrt{2}$

$sin \; 105^{o} \; + \; sin \; 15^{o} = \frac{1}{2} \sqrt{6} = \frac{\sqrt{6}}{2}$

Jawaban: E

Rumus Sin Selisih

Cara yang digunakan untuk menghafal rumus sin selisih sama seperti cara menghafal rumus sin jumlah, yaitu melalui sebuah kalimat. Kalimat tersbut adalah sin selisih sama dengan dua cos setengah jumlah sin setengah selisih. Persamaan rumus sin selisih dapat dilihat pada gambar di bawah.

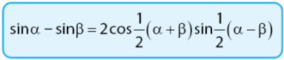
Rumus Selisih Fungsi Sin

Bukti:

Pada pembahasan rumus perkalian fungsi sinus dan cosinus, sudah terbukti bahwa:

$sin \; \left( A + B \right) - sin \; \left( A - B \right) = 2 \cdot cos \; A \cdot sin \; B$

Misalkan:

$\alpha = A + B$

$\beta = A - B$

Sehingga,

$\alpha + \beta = 2A \rightarrow A = \frac{1}{2}\left( \alpha + \beta \right)$

dan

$\alpha - \beta = 2B \rightarrow B = \frac{1}{2}\left( \alpha - \beta \right)$

Substitusi nilai A, B, $\alpha$ , dan $\beta$ pada rumus perkalian sinus dan cosinus, sehingga,

$sin \; \alpha - sin \; \beta = 2 \cdot cos \; \frac{1}{2}\left( \alpha + \beta \right) \cdot sin \; \frac{1}{2}\left( \alpha - \beta \right)$

Terbukti

Contoh soal dan pembahasan rumus sin selisih.

Diketahui besar sudut $\alpha = 105^{o}$ dan $\beta = 15^{o}$ . Nilai $sin \; 105^{o} \; + \; sin \; 15^{o}$ adalah ….

$\textrm{A.} \; \; \; \frac{\sqrt{2}}{6}$

$\textrm{B.} \; \; \; \frac{\sqrt{2}}{2}$

$\textrm{C.} \; \; \; \frac{\sqrt{3}}{6}$

$\textrm{D.} \; \; \; \frac{\sqrt{5}}{2}$

$\textrm{E.} \; \; \; \frac{\sqrt{6}}{2}$

Pembahasan:

$sin \; 105^{o} \; - \; sin \; 15^{o} = 2 \; cos \frac{1}{2} \left( 105^{o} + 15^{o} \right) \; sin \frac{1}{2} \left(105^{o} - 15^{o} \right)$

$sin \; 105^{o} \; - \; sin \; 15^{o} = 2 \; cos \frac{1}{2} \left( 120^{o} \right) \; sin \frac{1}{2} \left(90^{o} \right)$

$sin \; 105^{o} \; - \; sin \; 15^{o} = 2 \; cos \; 60^{o} \; sin \; 45^{o}$

$sin \; 105^{o} \; - \; sin \; 15^{o} = 2 \cdot \frac{1}{2} \cdot \frac{1}{2} \sqrt{2}$

$sin \; 105^{o} \; - \; sin \; 15^{o} = \frac{1}{2} \sqrt{2} = \frac{\sqrt{2}}{2}$

Jawaban: B

Rumus Cos Jumlah

Penjabaran yang ketiga adalah rumus cos jumlah. Penggunaannya hampir sama dengan kedua rumus yang telah dijabarkan sebelumnya. Kalimat untuk mengafal rumus cos jumlah adalah cos jumlah sama dengan dua cos setengah jumlah cos setengah selisih.

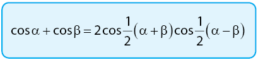
Rumus Penjumlahan Fungsi Sin

Bukti:

Pada pembahasan rumus perkalian fungsi sinus dan cosinus, sudah terbukti bahwa:

$cos \; \left( A + B \right) + cos \; \left( A - B \right) = 2 \cdot cos \; A \cdot cos \; B$

Misalkan:

$\alpha = A + B$

$\beta = A - B$

Sehingga,

$\alpha + \beta = 2A \rightarrow A = \frac{1}{2}\left( \alpha + \beta \right)$

dan

$\alpha - \beta = 2B \rightarrow B = \frac{1}{2}\left( \alpha - \beta \right)$

Substitusi nilai A, B, $\alpha$ , dan $\beta$ pada rumus perkalian sinus dan cosinus, sehingga,

$cos \; \alpha + cos \beta = 2 \cdot cos \; \frac{1}{2}\left( \alpha + \beta \right) \cdot cos \; \frac{1}{2}\left( \alpha - \beta \right)$

Terbukti

Contoh soal dan pembahasan rumus cos jumlah.

Diketahui besar sudut $\alpha = 105^{o}$ dan $\beta = 15^{o}$ . Nilai $cos \; 105^{o} \; + \; cos \; 15^{o}$ adalah ….

$\textrm{A.} \; \; \; \frac{\sqrt{2}}{6}$

$\textrm{B.} \; \; \; \frac{\sqrt{2}}{2}$

$\textrm{C.} \; \; \; \frac{\sqrt{3}}{6}$

$\textrm{D.} \; \; \; \frac{\sqrt{5}}{2}$

$\textrm{E.} \; \; \; \frac{\sqrt{6}}{2}$

Pembahasan:

$cos \; 105^{o} \; + \; cos \; 15^{o} = 2 \; cos \frac{1}{2} \left( 105^{o} + 15^{o} \right) \; cos \frac{1}{2} \left(105^{o} - 15^{o} \right)$

$cos \; 105^{o} \; + \; cos \; 15^{o} = 2 \; cos \frac{1}{2} \left( 120^{o} \right) \; cos \frac{1}{2} \left(90^{o} \right)$

$cos \; 105^{o} \; + \; cos \; 15^{o} = 2 \; cos \; 60^{o} \; cos \; 45^{o}$

$cos \; 105^{o} \; + \; cos \; 15^{o} = 2 \cdot \frac{1}{2} \cdot \frac{1}{2} \sqrt{2}$

$cos \; 105^{o} \; + \; cos \; 15^{o} = \frac{1}{2} \sqrt{2} = \frac{\sqrt{2}}{2}$

Jawaban: B

Rumus Cos Selisih

Selanjutnya adalah penjabaran mengenai rumus cos selisih. Kalimat yang digunakan untuk menghafal rumus cos selisih adalah cos selisih sama dengan min dua sin setengah jumlah sin setengah selisih. Bentuk rumus cos selisih dapat dilihat pada gambar di bawah.

Rumus Selisih Cos

Bukti:

Pada pembahasan rumus perkalian fungsi sinus dan cosinus, sudah terbukti bahwa:

$cos \; \left( A + B \right) - cos \; \left( A - B \right) = -2 \cdot sin \; A \cdot sin \; B$

Misalkan:

$\alpha = A + B$

$\beta = A - B$

Sehingga,

$\alpha + \beta = 2A \rightarrow A = \frac{1}{2}\left( \alpha + \beta \right)$

dan

$\alpha - \beta = 2B \rightarrow B = \frac{1}{2}\left( \alpha - \beta \right)$

Substitusi nilai A, B, $\alpha$ , dan $\beta$ pada rumus perkalian sinus dan cosinus, sehingga,

$cos \; \alpha - cos \; \beta = -2 \cdot sin \; \frac{1}{2}\left( \alpha + \beta \right) \cdot sin \; \frac{1}{2}\left( \alpha - \beta \right)$

Terbukti

Contoh soal dan pembahasan rumus cos selisih.

Diketahui besar sudut $\alpha = 105^{o}$ dan $\beta = 15^{o}$ . Nilai $cos \; 105^{o} \; + \; cos \; 15^{o}$ adalah ….

$\textrm{A.} \; \; \; -\frac{\sqrt{2}}{6}$

$\textrm{B.} \; \; \; -\frac{\sqrt{2}}{2}$

$\textrm{C.} \; \; \; -\frac{\sqrt{3}}{6}$

$\textrm{D.} \; \; \; -\frac{\sqrt{5}}{2}$

$\textrm{E.} \; \; \; -\frac{\sqrt{6}}{2}$

Pembasan:

$cos \; 105^{o} \; - \; cos \; 15^{o} = -2 \; sin \frac{1}{2} \left( 105^{o} + 15^{o} \right) \; sin \frac{1}{2} \left(105^{o} - 15^{o} \right)$

$cos \; 105^{o} \; - \; cos \; 15^{o} = -2 \; sin \frac{1}{2} \left( 120^{o} \right) \; sin \frac{1}{2} \left(90^{o} \right)$

$cos \; 105^{o} \; - \; cos \; 15^{o} = -2 \; sin \; 60^{o} \; sin \; 45^{o}$

$cos \; 105^{o} \; - \; cos \; 15^{o} = -2 \cdot \frac{1}{2} \sqrt{3} \cdot \frac{1}{2} \sqrt{2}$

$cos \; 105^{o} \; - \; cos \; 15^{o} = - \frac{1}{2} \sqrt{6} = -\frac{\sqrt{6}}{2}$

Jawaban: E

Trending

Kalkulus Dasar: Limit, Turunan, dan Integral

Statistika Data Kelompok

Ukuran Pemusatan, Letak & Sebaran Data

Memodelkan dengan Sistem Persamaan Linear

Peluang Suatu Kejadian

Menikmati Senja Pantai Wediombo di Rumah Panggung Taman Keben

Fungsi Komposisi dan Invers

Penasaran Dengan Grup Band South Hill ???

Rangkuman Materi Pembelajaran Trigonometri Kelas 10 SMK

Nilai Fungsi Trigonometri Sudut Istimewa

Identitas Trigonometri (Identitas Pythagoras)

Grafik Fungsi Trigonometri

1. Grafik fungsi sinus (y = a sin bx, x ∈ [0^o, 360^o])

3. Grafik fungsi tangen (y = tan x, x ∈ [0^o, 360^o])

Contoh Soal 1

Contoh Soal 2

Contoh Soal 3

Aturan Sinus dan Cosinus: Rumus & Contoh Soal

Aturan Sinus

Contoh Soal Aturan Sinus

Aturan Cosinus

Contoh Soal Aturan Cosinus

Penggunaan Trigonometri dalam Menentukan Luas Segitiga

Diketahui Alas dan Tinggi Segitiga

Luas Segitiga yang Diketahui Dua Sisi dan Sudut yang Diapitnya

Luas Segitiga yang Diketahui Dua Sudut dan Satu Sisi Diketahui

Luas Segitiga yang Diketahui Ketiga Sisinya

Rumus Sin Selisih

Rumus Cos Jumlah

Rumus Cos Selisih

Post a Comment

Contact Form

Rangkuman Materi Pembelajaran Trigonometri Kelas 10 SMK

Nilai Fungsi Trigonometri Sudut Istimewa

Identitas Trigonometri (Identitas Pythagoras)

Grafik Fungsi Trigonometri

1. Grafik fungsi sinus (y = a sin bx, x ∈ [0o, 360o])

3. Grafik fungsi tangen (y = tan x, x ∈ [0o, 360o])

Contoh Soal 1

Contoh Soal 2

Contoh Soal 3

Aturan Sinus dan Cosinus: Rumus & Contoh Soal

Aturan Sinus

Contoh Soal Aturan Sinus

Aturan Cosinus

Contoh Soal Aturan Cosinus

Penggunaan Trigonometri dalam Menentukan Luas Segitiga

Diketahui Alas dan Tinggi Segitiga

Luas Segitiga yang Diketahui Dua Sisi dan Sudut yang Diapitnya

Luas Segitiga yang Diketahui Dua Sudut dan Satu Sisi Diketahui

Luas Segitiga yang Diketahui Ketiga Sisinya

Rumus Sin Selisih

Rumus Cos Jumlah

Rumus Cos Selisih

Post a Comment

Contact Form

1. Grafik fungsi sinus (y = a sin bx, x ∈ [0^o, 360^o])

3. Grafik fungsi tangen (y = tan x, x ∈ [0^o, 360^o])