
Persamaan Garis lurus yaitu suatu perbandingan antara koordinat y dan koordinat x dari dua titik yang terletak pada sebuah garis. Sedangkan garis lurus sendiri ialah kumpulan dari titik – titik yang sejajar. Dan garis lurus dapat dinyatakan dalam berbagai bentuk.
Dibawah ini beberapa contoh untuk menyatakan persamaan garis lurus, yaitu :
- y = mx
- y = -mx
- y = a
- x = a
- ax + by = ab
- ax – by = -ab
- dan lain-lain
Perhatikan gambar dibawah ini beberapa contoh grafik dan bentuk garis lurus serta cara menyatakan atau menentukannya :
Gradien yaitu Perbandingan komponen y dan komponen x , atau disebut juga dengan kecondongan sebuah garis. Lambang dari suatu gradien yaitu huruf “m”.
Gradien juga dapat dinyatakan sebagai nilai dari kemiringan suatu garis dan dapat dinyatakan dengan perbandingan Δy/Δx
Perhatikan gambar dibawah ini untuk menentukan gradien pada sebuah persamaan garis berikut :
Berikut ini rumus mencari gradien garis dengan beberapa jenis persamaan :
- Gradien dari persamaan ax + by + c = 0
- Gradien yang melalui titik pusat ( 0 , 0 ) dan titik ( a , b )m = b/a
m = b/a
- Gradien Yang melalui titik ( x1 , y 1 ) dan ( x2 , y2 )
m = y1 – y2 / x1 – x2 atau m = y2 – y1 / x2 – x1
- Gradien garis yang saling sejajar ( / / )
m = sama atau jika dilambangkan adalah m1 = m2
- Gradien garis yang saling tegak lurus ( lawan dan kebalikan )
m = -1 atau m1 x m2 = -1
Rumus Cara Menentukan
1. Persamaan Garis Lurus bentuk umum ( y = mx ) Persamaan yang melalui titik pusat ( 0 , 0 ) dan bergradien m .
Contoh :
Tentukan persamaan garis lurus yang melalui titik pusat ( 0 , 0 ) dan bergradien 2 !
Jawab : y = mx
y = 2 x
2. y = mx + c
->Persamaan garis yang / / dengan y = mx dan bergradien m
-> Persamaan garis yang melalui titik ( 0 , c ) dan bergradien m. ( 0 , c ) adalah titik potong sumbu y .
3. Persamaan Garis Lurus Yang Melalui titik ( x1 , y1 ) dan bergradien m
persamaannya yaitu :
y – y1 = m ( x – x1 )
4. Persamaan Garis Lurus Yang Melaui Dua titik yaitu ( x1 , y 1 ) dan ( x2 , y2 ) .
Contoh Soal:
Gambarlah grafik dari persamaan garis lurus y = 3x - 9!
1. Cari titik potong di sumbu x
Cara mencari titik potong pada sumbu x adalah dengan membuat variabel y menjadi 0.

Jadi, saat y = 0, nilai x yang dihasilkan adalah 2. Sehingga, diperoleh titik potong di sumbu x adalah (3,0).

2. Cari titik potong di sumbu y
Tidak jauh berbeda dengan cara mencari titik potong pada sumbu x, untuk mencari titik potong di sumbu y, kita harus mengganti variabel x menjadi 0.

Jadi, saat x = 0, nilai y yang dihasilkan adalah -6. Sehingga, diperoleh titik potong di sumbu y adalah (0,-9).

3. Gambar garis yang menghubungkan titik potong tersebut
Setelah diperoleh dua buah titik potongnya, kita bisa tarik garis lurus yang menghubungkan kedua titik potong tersebut. Sehingga, hasilnya akan seperti ini.










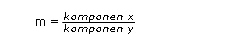
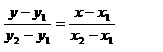
Post a Comment